24
G
RAPHING
T
ECHNOLOGY
G
UIDE
: TI-82
Copyright © Houghton Mifflin Company. All rights reserved.
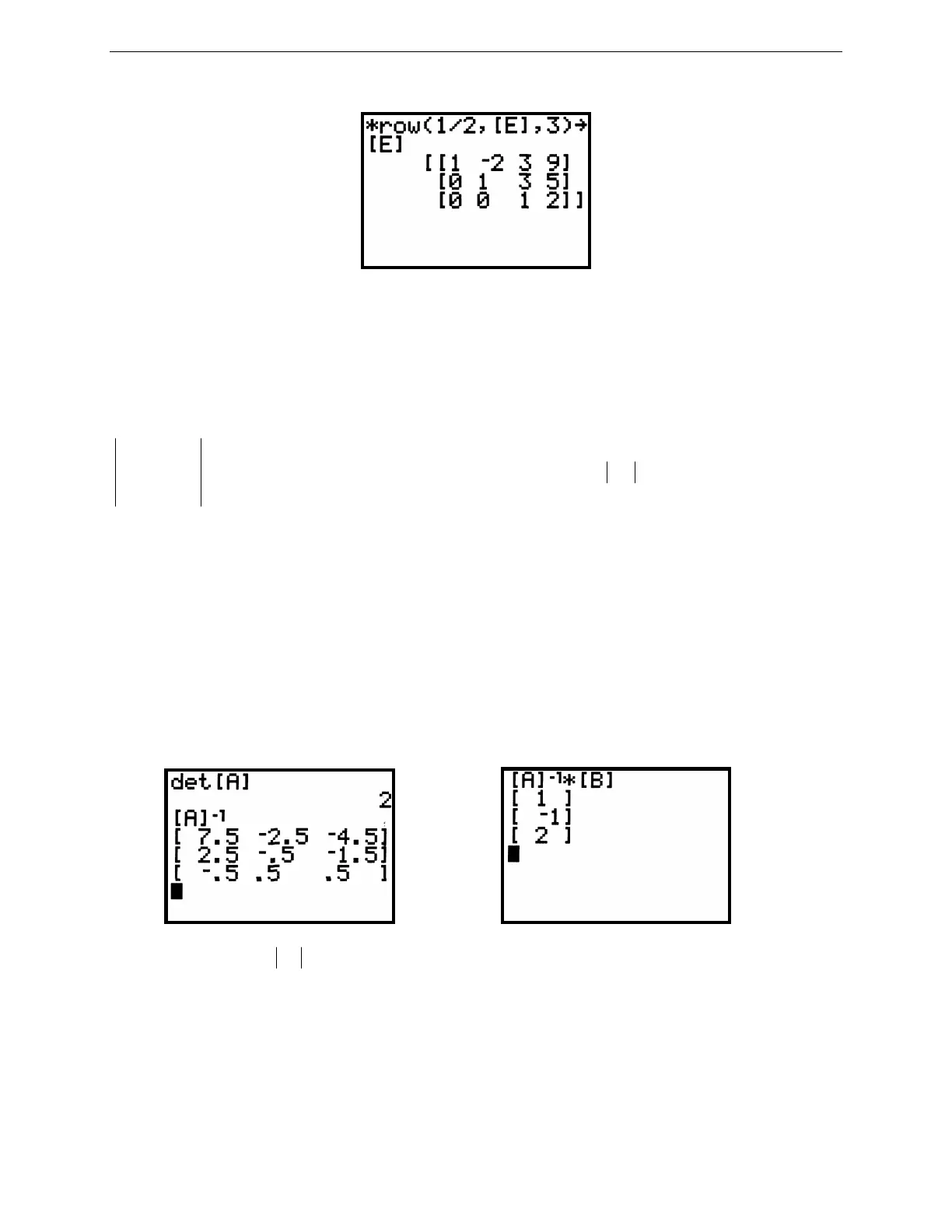
Figure 2.67: Final matrix after row operations
Thus z = 2, so y = –1 and x = 1.
2.6.4 Determinants and Inverses: Enter this 3×3 square matrix as [A]:
123
130
255
−
−
−
. To calculate its determinant,
123
130
255
−
−
−
, press MATRX ► 1 MATRX 1 ENTER. You should find that
[]
A = 2, as shown in Figure 2.68.
Since the determinant of matrix [A] is not zero, it has an inverse, [A]
–1
. Press MATRX 1 x
-1
ENTER to calculate the
inverse of matrix [A], also shown in Figure 2.68.
Now let’s solve a system of linear equations by matrix inversion. Once more, consider
239
34
25517
xyz
xy
xyz
−+=
−+ =−
−+=
The coefficient matrix for this system is the matrix
123
130
255
−
−
−
that was entered in the previous example.
Figure 2.68:
[]
A
and [A]
–1
Figure 2.69: Solution matrix
If necessary, enter it again as [A] in your TI-82. Enter the matrix
9
4
17
−
as [B]. Then press MATRX 1 x
-1
× MATRX
2 ENTER to calculate the solution matrix (Figure 2.69). The solutions are still x = 1, y = –1, and z = 2.
To Next Page
Loading...
Need help?
General
