164 Section 12: Calculating with Matrices
Matrix A now represents the complex matrix Z in Z
P
form:
A = Z
P
=
4 7
1 3
3
−
2
5 8
.
The Complex Transformations Between Z
P
and Z
An additional transformation must be done when you want to calculate
the product of two complex matrices, and still another when you want to
calculate the inverse of a complex matrix. These transformations convert
between the Z
P
representation of an m × n complex matrix and a 2m × 2n
partitioned matrix of the following form:
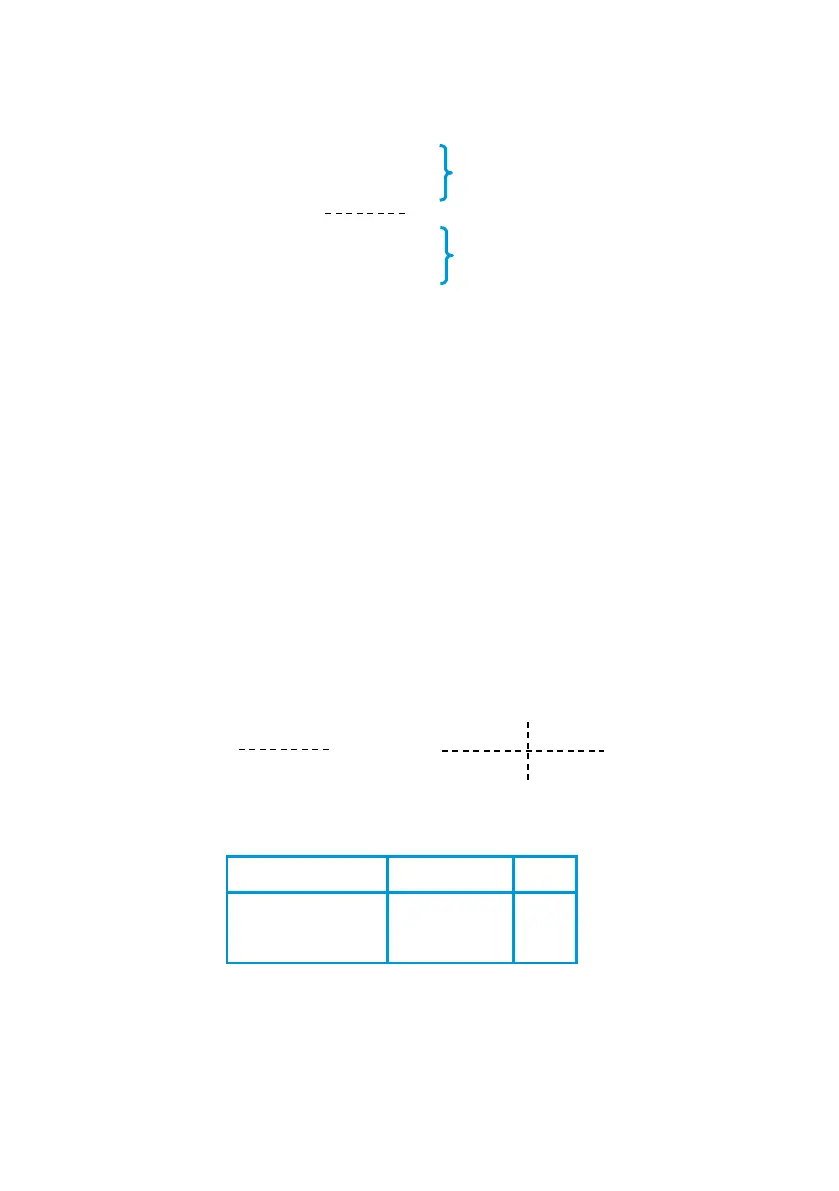
Z =
X
−
Y
Y X
.
The matrix Z created by the > 2 transformation has twice as many
elements as Z
P
.
For example, the matrices below show how Z is related to Z
P
.
Z
P
=
1
−
6
−
4 5
Z =
1
−
6 4
−
5
−
4 5 1
−
6
.
The transformations that convert the representation of a complex matrix
between Z
P
and Z are shown in the following table.
Pressing Transforms
Into
´ > 2
Z
P
Z
´ > 3
Z Z
P
To do either of these transformations, recall the descriptor of Z
P
or Z into
the display, then press the keys shown above. The transformation is done
to the specified matrix; the result matrix is not affected.
Real Part
Imaginary Part
To Next Page
Loading...
Need help?
General
