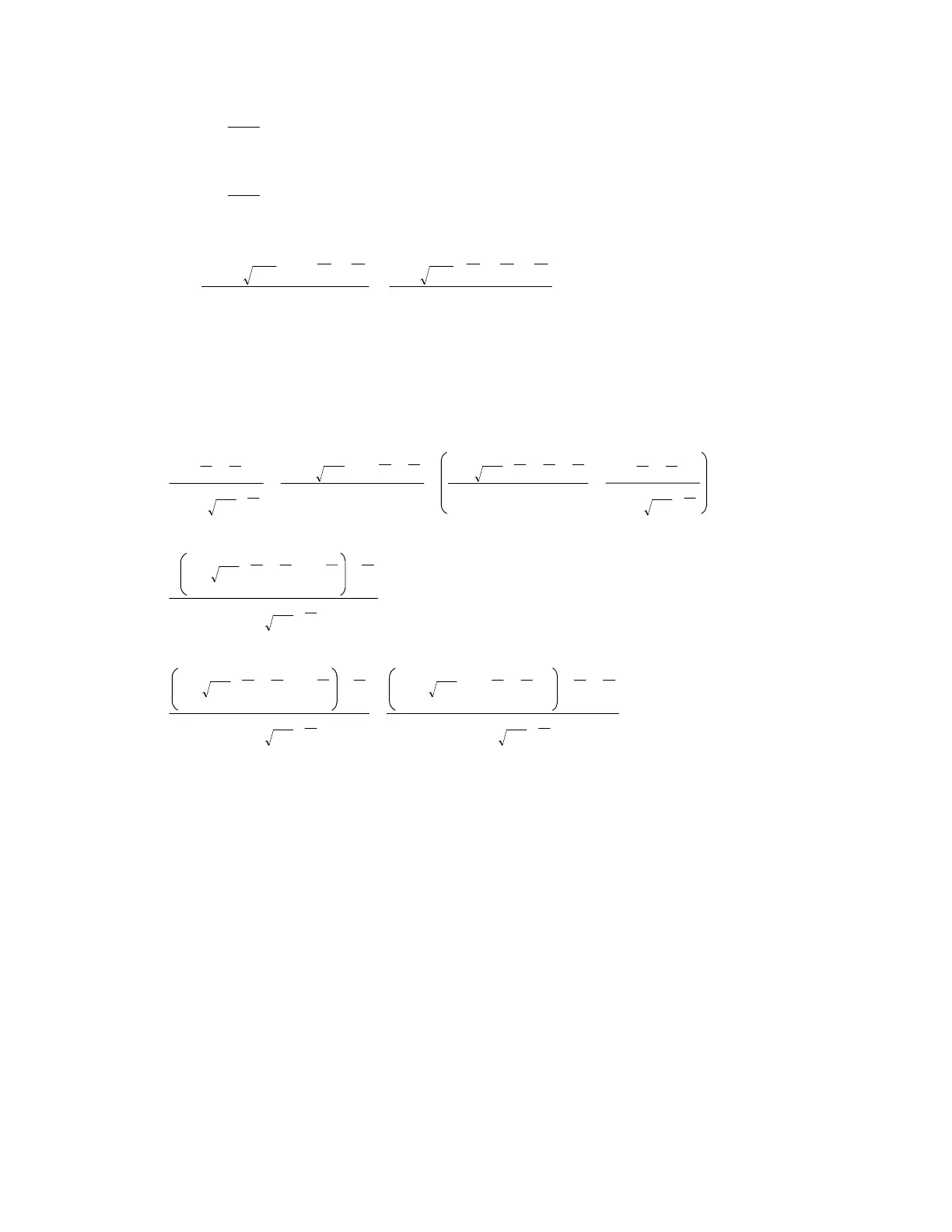✍ = ✬ +
$
✎ = ✬ −
3$✬
✬ =
(
−3$
(
69 −9
))
1
3
$2
2
3
12
+
(
9− 69
)
1
3
$3
5
6
$2
2
3
12
$ i
The first three elements are the solutions to the cubic polynomial. The last three elements define the
variable substitutions used in the solutions. This format reduces the size of the output list, and makes
the solutions more intelligible. The function evalrt() automatically applies these substitutions. evalrt() is
called with the solution list output from cubic(), with these results returned as a list:
3
2
3
$2
1
3
6$
(
9− 69
)
1
3
+
(
−3$
(
69
−9
))
1
3
$2
2
3
12
+
(
9− 69
)
1
3
$3
5
6
$2
2
3
12
−
3
1
6
$2
1
3
2$
(
9− 69
)
1
3
$ i
−
(
9− 69
)
2
3
$2
1
3
+2$3
1
3
$6
1
3
6
$
(
9− 69
)
1
3
(
9− 69
)
2
3
$2
1
3
+2$3
1
3
$6
1
3
12
$
(
6− 69
)
1
3
−
(
−3$
(
69
−9
))
2
3
$2
1
3
−6
$3
1
6
$2
1
3
12
$
(
9− 69
)
1
3
$ i
These solutions can be verified by substituting them back into the original polynomial.
For another example, try quartic(x
4
-x+1,x). The results are quite long, and not shown here. Since they
involve inverse trigonometric functions, they cannot be checked by substituting them into the original
polynomial. However, if they are substituted into the original polynomial and approximate results are
found, those results are zero to within machine precision.
If the polynomial to be solved has complex coefficients, you must specify that the argument variable is
complex with the underscore character "_", or the complex solutions will not be returned. For example,
solve the polynomial generated by
(
x + 2
)
$
(
x − 3
)
$
(
x − 7i
)
which obviously has roots of -2, 3 and 7i. This expression expands to
x
(
x − 3
)(
x + 2
)
− 7
(
x − 3
)(
x + 2
)
i
6 - 13
To Next Page
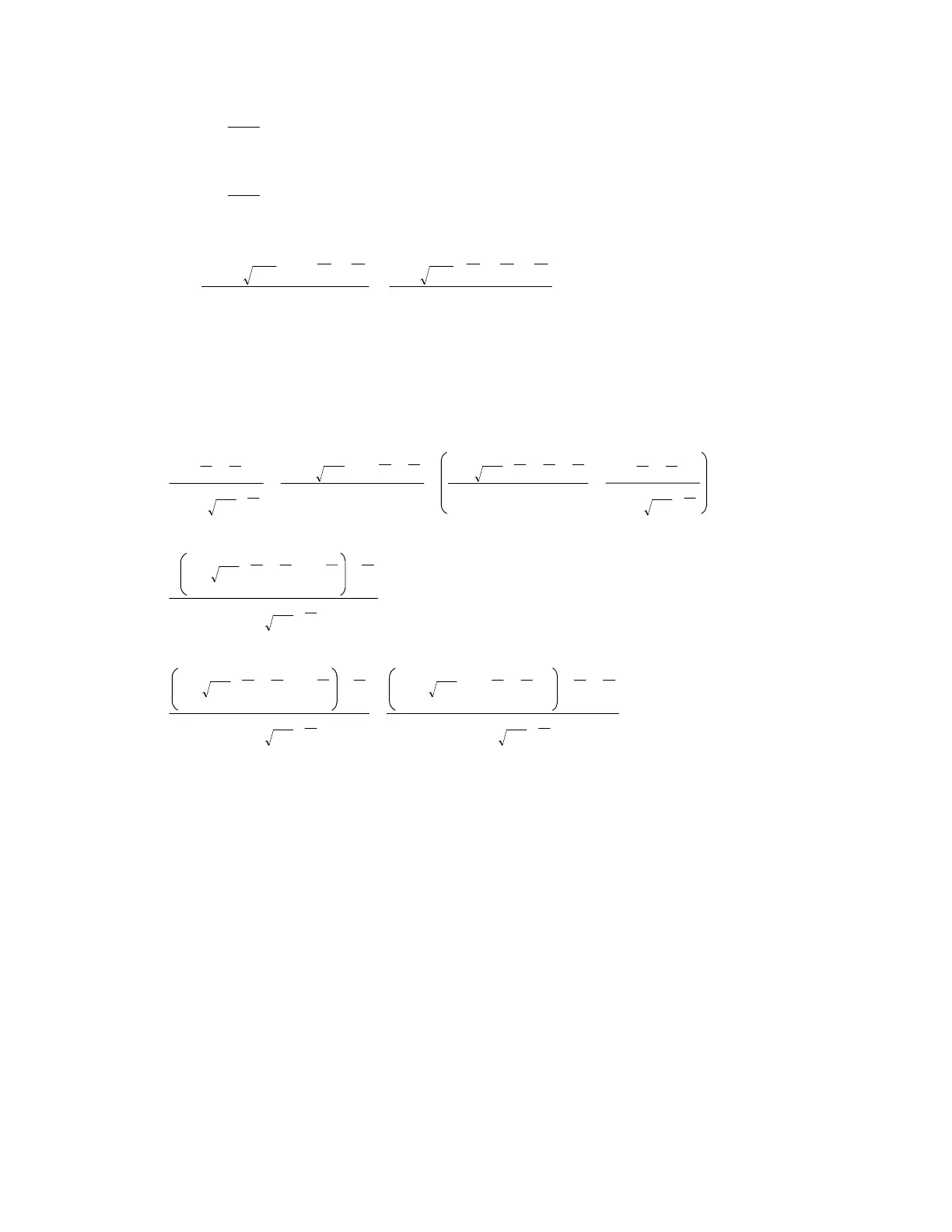Loading...
Need help?
General
