21
13
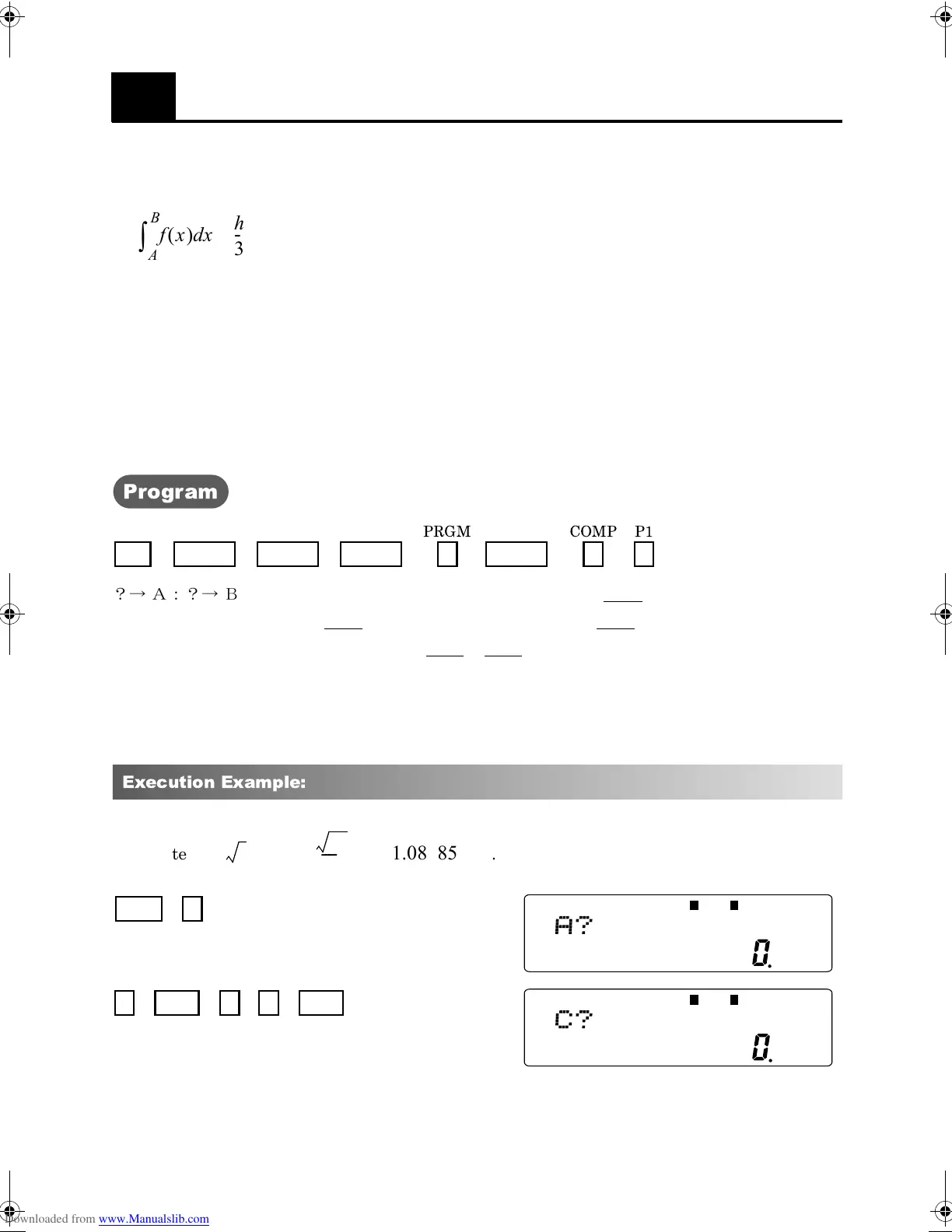
Definite integrals
(Simpsons formula)
The value of a definite integral can be approximated by Simpsons formula,
:number of stripes
As becomes larger the approximation becomes better, and the limit as approaches
infinity is consistent with the true answer.
In general, this method gives good approximations.
Program
?→ A:?→ B:?→ C:1→ D:(B-A)÷2C→M:√A→ Y:Lbl 1:A +
2DM-M→X:Y+4√X
→Y:X+M→X:Y+2√X→ Y:D +1→ D:C >
D⇒Goto 1:B-M→X:Y+4√X
+√ B → Y:YM ÷3→ Y:Y < 105 STEP >
INPUT A,B : interval of integration [
A
,
B
] C: number of stripes
OUTPUT Y : value of the definite integral
Execution Example:
Calculate .
fx()xd
A
B
∫
h
3
---
fA() fB() 4 fA 2i 1–()h+()
i 1=
n
∑
2 fA 2ih+()
i 1=
n 1–
∑
++ +
≈
h
BA–
2n
-------------= n
nn
ON
MODE MODE MODE
1
PRGM
MODE
1
COMP
1
P1
xxd
0
10
∫
10
20
3
-------------- 21.08185107==
Prog
1
S A
D R
P1
P2 P3 P4
G
0
EXE
1 0
EXE
S A
D R
P1
P2 P3 P4
G
関数電卓事例集 .book 21 ページ 2002年9月2日 月曜日 午後6時51分

 Loading...
Loading...