Casio fx-3650P

27
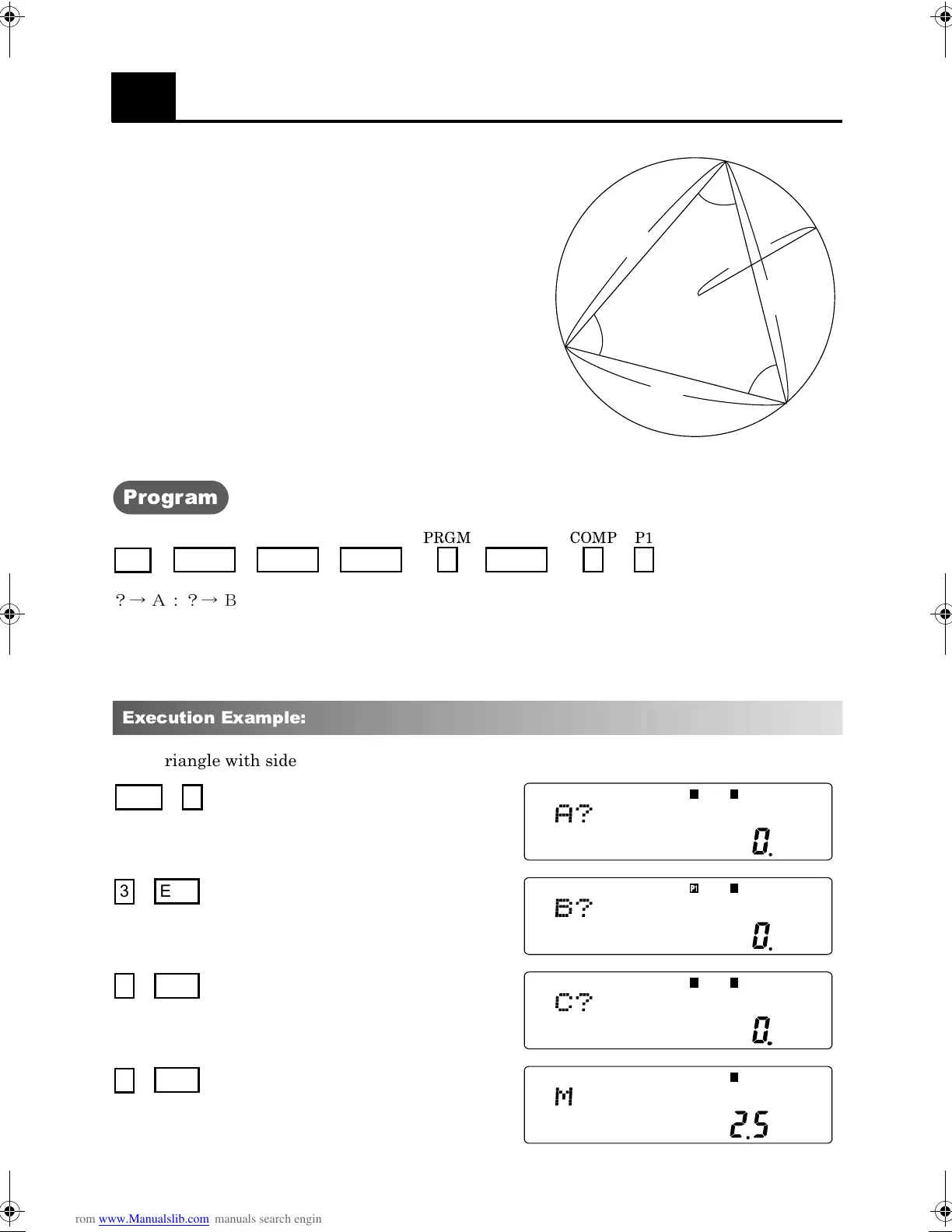
18 The radius of the Circumscribed circle
The law of sines：For △ ABC , as shown in the
diagram on the right, the following formula holds:
It is thereby possible, by the law of cosines and law of
sines, to calculate the radius of the circumscribed
circle given the lengths of the three sides of the
triangle.
Program
？→ Ａ：？→ Ｂ：？→ Ｃ：ｓｉｎ ｃｏｓ
－１
（（Ｂ
２
＋Ｃ
２
－Ａ
２
）÷２ ＢＣ）→ Ｄ：
Ａ÷２Ｄ→Ｍ：Ｍ ＜41 STEP ＞
OUTPUT Ｍ : the radius of the circumscribed circle
Execution Example:
For a triangle with sides if length 3, 4 and 5, the radius of the circumscribed circle is 2.5:
a
Asin
-----------
b
Bsin
-----------
c
Csin
----------- 2R===
A
B
a
c
b
C
R
R
A
2
1–
cos
B
2
C
2
A
2
–+
2BC
-------------------------------


sin
-------------------------------------------------------------
=
ON
MODE MODE MODE
1
PRGM
MODE
1
COMP
1
P1
Prog
1
S A
D R P1
P1
P2 P3 P4 G
3
EXE
S A
D R P1
P1
P2 P3 P4 G
4
EXE
S A
D R P1
P1
P2 P3 P4 G
888888888
88
8 8 8 8 8 8 8 8 8 8
5
EXE
M
S A
D R P1
P1
P2 P3 P4 G
関数電卓事例集 .book 27 ページ ２００２年９月２日 月曜日 午後６時５１分