Casio fx-3650P

4
02 Fractions from recurring decimals
Recurring decimals may be converted to fraction by proceeding in the following way:
= 0.111111111111 = 0.01010101010
= 0.001001001001001 = 0.000100010001
For example, 0.345345345…… is
0.345345345 …… =
Program
？→ Ａ：？→ Ｂ：１０＾ Ａ －１→ Ａ：Ａ → Ｘ：Ｂ → Ｙ：Ｌｂｌ １：Ａ － Ｂ → Ａ：Ａ ≧
Ｂ ⇒ Ｇｏｔｏ １：Ａ ＝０⇒ Ｇｏｔｏ ２：Ａ → Ｃ：Ｂ → Ａ：Ｃ → Ｂ：Ｇｏｔｏ １：Ｌｂｌ
２：Ｙ ÷ Ｂ Ｘ÷Ｂ ＜73 STEP ＞
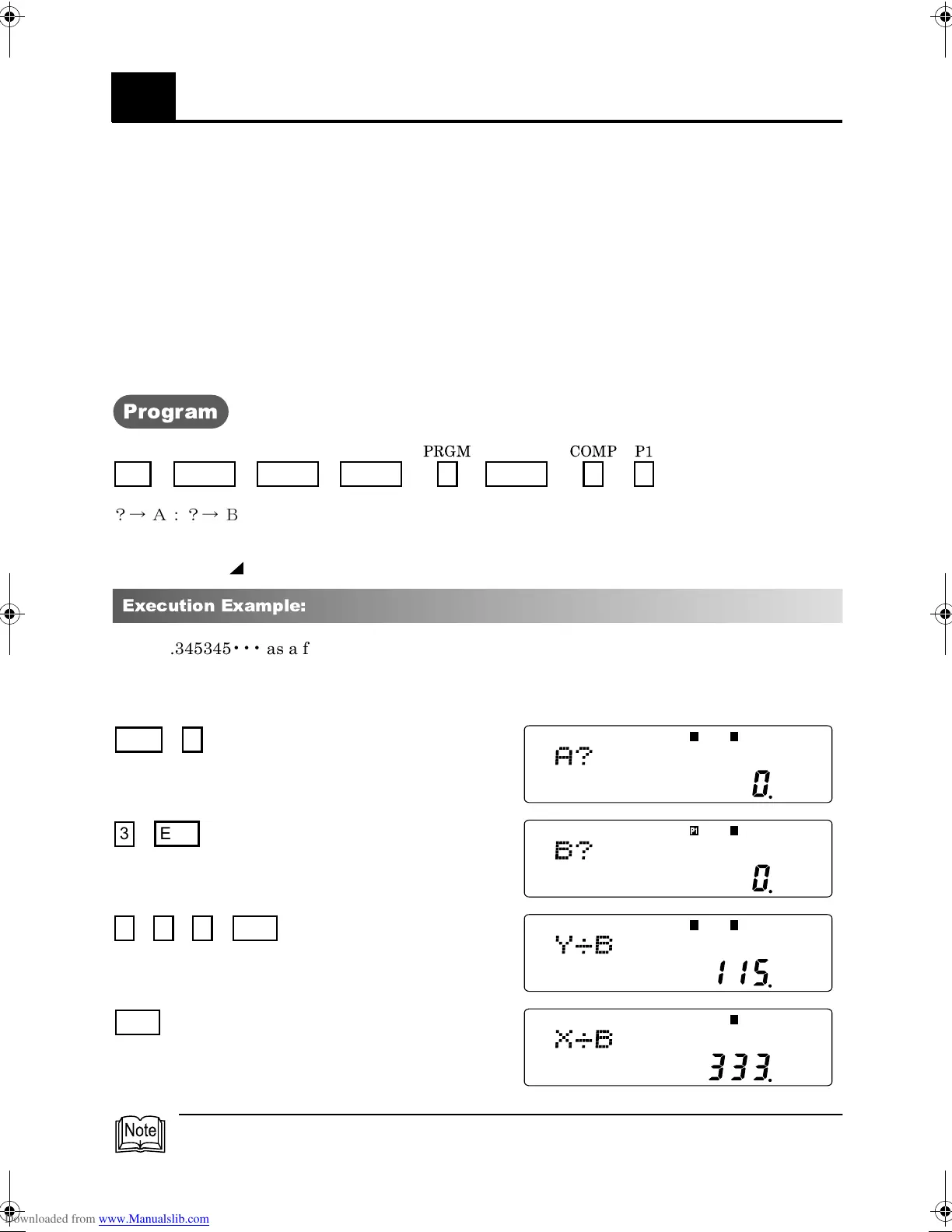
Execution Example:
Write 0.345345••• as a fraction.
Ａ？ : The number of digits in the repeated pattern (e.g. 3 in the example)
Ｂ？ : The recurring sequence of digits (e.g. 345 in the example)
*This program deals only with the case in which the 1st to Ath digits immediately following
the decimal point are repeated.
i.e. 0.033333...= 1/30 and 0.166666...= 1/6 cannot be converted.
1
9
---
……
1
99
------
……
1
999
---------
……
1
9999
------------
……
345
999
---------
115
333
---------
=
ON
MODE MODE MODE
1
PRGM
MODE
1
COMP
1
P1
Prog
1
S A
D R P1
P1
P2 P3 P4 G
3
EXE
S A
D R P1
P1
P2 P3 P4 G
3 4 5
EXE
Disp
S A
D R P1
P1
P2 P3 P4 G
EXE
S A
D R P1
P1
P2 P3 P4 G
関数電卓事例集 .book 4 ページ ２００２年９月２日 月曜日 午後６時５１分