39
28
T
est on a mean with known
(z-tests)
σ
2
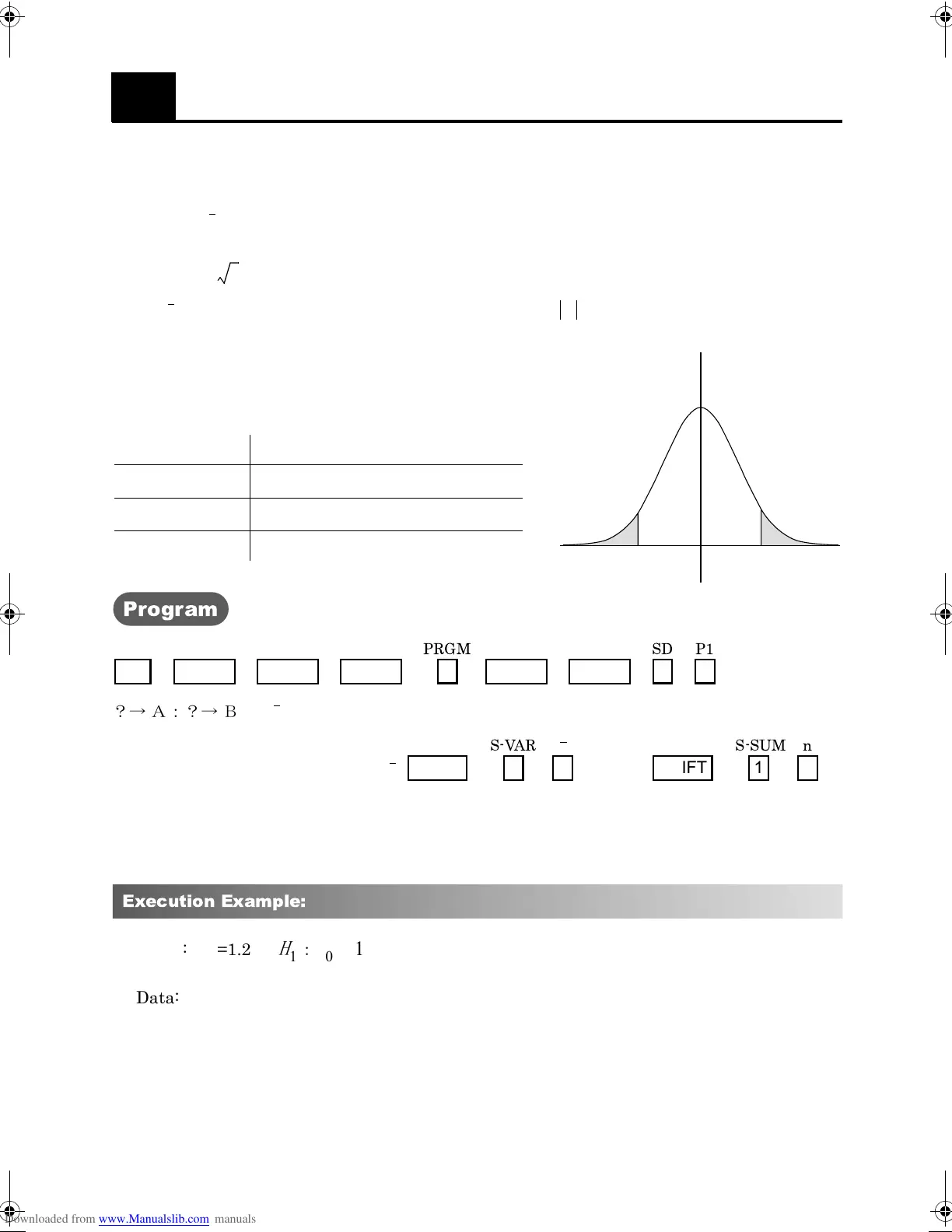
The hypothesis of interest is that the mean is equal to a given value , versus the
alternative that it is not equal to . We calculate the test statistics
where is the sample mean and is the sample size. If , we reject the hypothesis
for the significance level .
For different significance levels, the confidence limits
are given below:
Program
?→ A:?→ B:( - A)÷√(B ÷ )→ C:C < 24 STEP >
:
:
`
INPUT A: given value B:population variance
OUTPUT C: value of Z
Execution Example:
Test : =1.2 :
Data: 1.4, 1.5, 1.3, 1.4, 1.7, 1.5, 1.3 Population variance =0.02
µ
0
µ
0
Z
x
µ
–
σ
n
-------
------------=
x nZ1.96≥
α
0.05=
α Confidence limits
0.10 1.64
0.05 1.96
0.01 2.57
1.96
0
-1.96
ON
MODE MODE MODE
1
PRGM
MODE MODE
1
SD
1
P1
x n
x
SHIFT
2
S-VAR
1
x
n
SHIFT
1
S-SUM
3
n
µ
0
σ
2
H
0
µ
0
H
1
µ
0
1.2≠
σ
2
関数電卓事例集 .book 39 ページ 2002年9月2日 月曜日 午後6時51分

 Loading...
Loading...