Casio fx-3650P

26
17 The radius of the Inscribed circle.
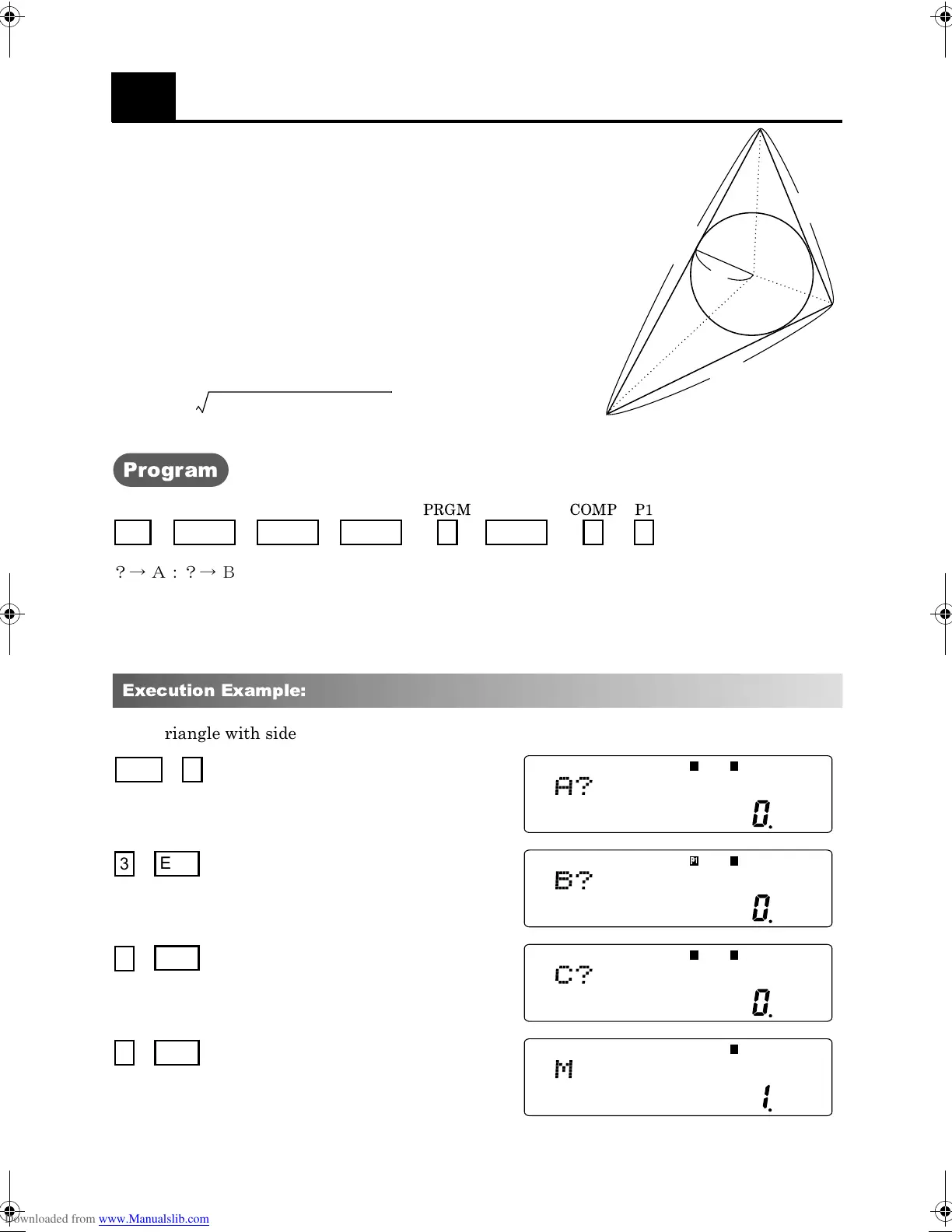
The inscribed circle is shown in the diagram on the
right.When the inscribed circle has radius , the area of
the appropriate triangle is:
Now, using herons formula it is possible to determine
the area of the triangle in terms of the length of the
three sides, whereby the radius of the circle is:
,
Program
？→ Ａ：？→ Ｂ：？→ Ｃ：（Ａ ＋ Ｂ ＋ Ｃ）÷２→ Ｄ：√（Ｄ（Ｄ － Ａ）（Ｄ － Ｂ）（Ｄ－Ｃ））
÷ Ｄ → Ｍ：Ｍ ＜ 49 STEP ＞
OUTPUT Ｍ : the radius of the inscribed circle
Execution Example:
For a triangle with sides of length 3, 4 and 5, the radius of the inscribed circle is 1:
R
S
AR
2
------
BR
2
------
CR
2
------++
ABC ++() R
2
-----------------------------==
A
B
C
R
R
DD A –() DB –() DC –()
D
----------------------------------------------------------= D
ABC ++
2
---------------------=
ON
MODE MODE MODE
1
PRGM
MODE
1
COMP
1
P1
Prog
1
S A
D R P1
P1
P2 P3 P4 G
3
EXE
S A
D R P1
P1
P2 P3 P4 G
4
EXE
S A
D R P1
P1
P2 P3 P4 G
5
EXE
M
S A
D R P1
P1
P2 P3 P4 G
関数電卓事例集 .book 26 ページ ２００２年９月２日 月曜日 午後６時５１分