Texas Instruments TI-85 - Page 20

Now press the keys STAT  1 L1 , L2
ENTER and you see
The first number you see is the mean ¯x = 2.52.
Further down the list is the standard deviation σ
x
=
1.081480467.
Section 11.2 in Text
Line Plots and Histograms
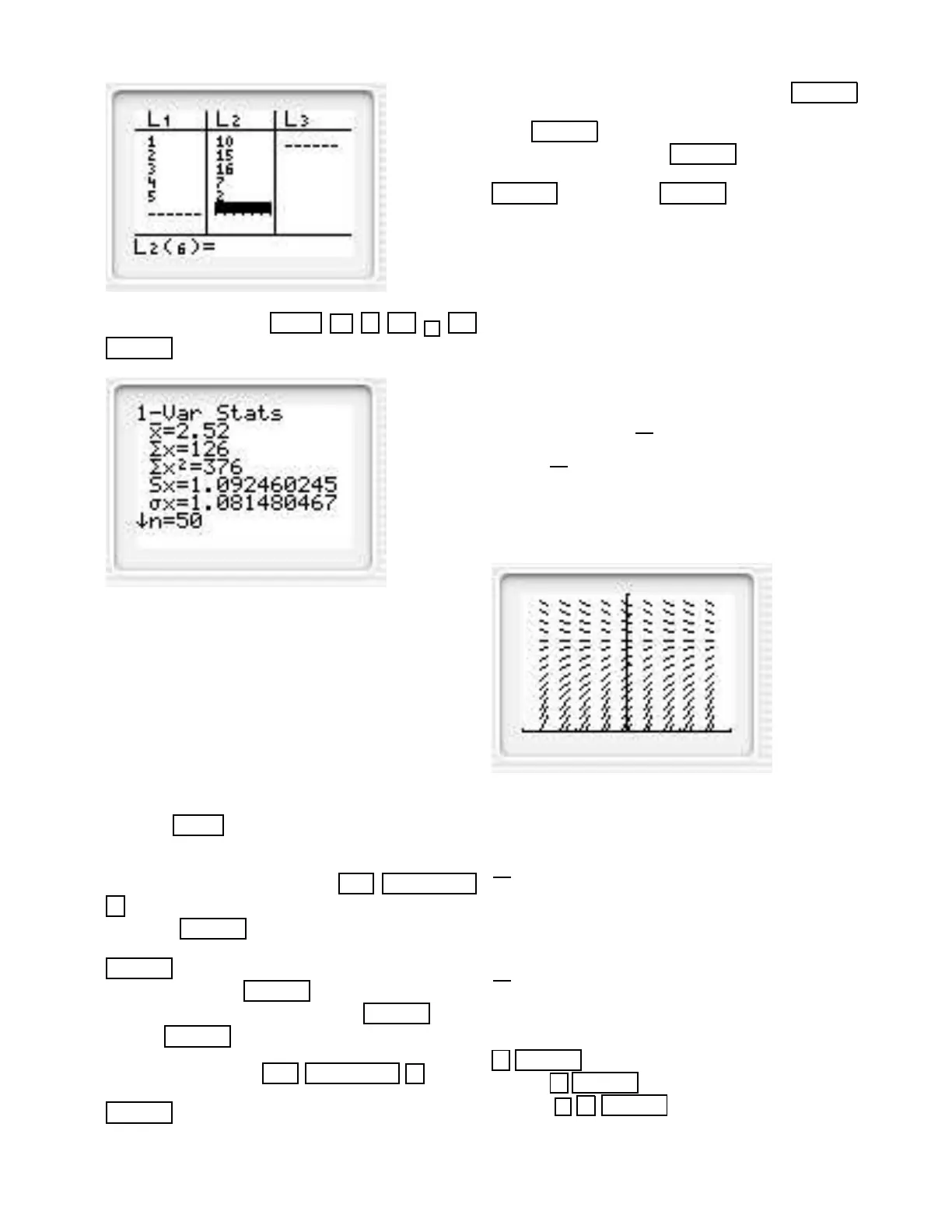
Reproduce Figure 11.7 in the text.
Solution. Set the dimensions of the viewing window
to [64, 76] by [0, 1500], with Xscl= 1. After pressing
the keys STAT 1, enter the data 64.5, 65.5, 66.5,
67.5, . . . in the first column, and enter the frequency
(NOT probability) data 385, 439, 794, 1070, . . . in the
second column. Press the keys 2nd STATPLOT
1 . Place the blinking cursor over On in the first line
and press ENTER . Place the blinking cursor over
the histogram (last item) in the second line and press
ENTER . Place the blinking cursor over L1 in the
third line and press ENTER . Place the blinking cur-
sor over L2 in the fourth line and press ENTER . Press
the key TRACE and you obtain Figure 11.6 in the
text.
Now press the keys 2nd STATPLOT 2 . Place
the blinking cursor over On in the first line and press
ENTER . Place the blinking cursor over the line plot
(second item) in the second line and press ENTER .
Place the blinking cursor over L1 in the third line and
press ENTER . Place the blinking cursor over L2 in
the fourth line and press ENTER . Place the blink-
ing cursor over the last item in the fifth line and press
ENTER . Press the key TRACE and you obtain Fig-
ure 11.7 in the text.
Section 12.3 in Text
• The Program DFIELD
• The Program EULER
• The Program EULERG
The Program DFIELD
The program DFIELD draws a direction field for the
differential equation
dy
dx
= f(x, y). Find the direction
field for
dy
dx
= 4 −y. (Refer to Example 1 in the text.)
Solution. Input Y
1
= 4 − Y . Use a window with
dimensions [−2, 2] by [0, 6]. Execute the program
DFIELD. A sketch of the direction field will appear.
The Program EULER
The program EULER executes Euler’s method . Exe-
cute the program EULER for the differential equation
dy
dx
= −y + x + 1 with initial condition y(0) = 1. (Refer
to Example 3 in the text.)
Solution. We want to use the program EULER to
approximate the solution to the initial value problem
dy
dx
= −y + x + 1, y(0) = 1, on the interval [0, 1] by
taking h = 0.2.
Input Y
1
= −Y + X + 1. Execute the program EU-
LER. The value x0, or x
0
is requested. Press the keys
0 ENTER . The value y0, or y
0
is requested. Press
the keys 1 ENTER . The value H is requested. Press
the keys . 2 ENTER . The value B is requested.
49