FCP manual
Code +030220391 – rel 1.2 25/03/08
17
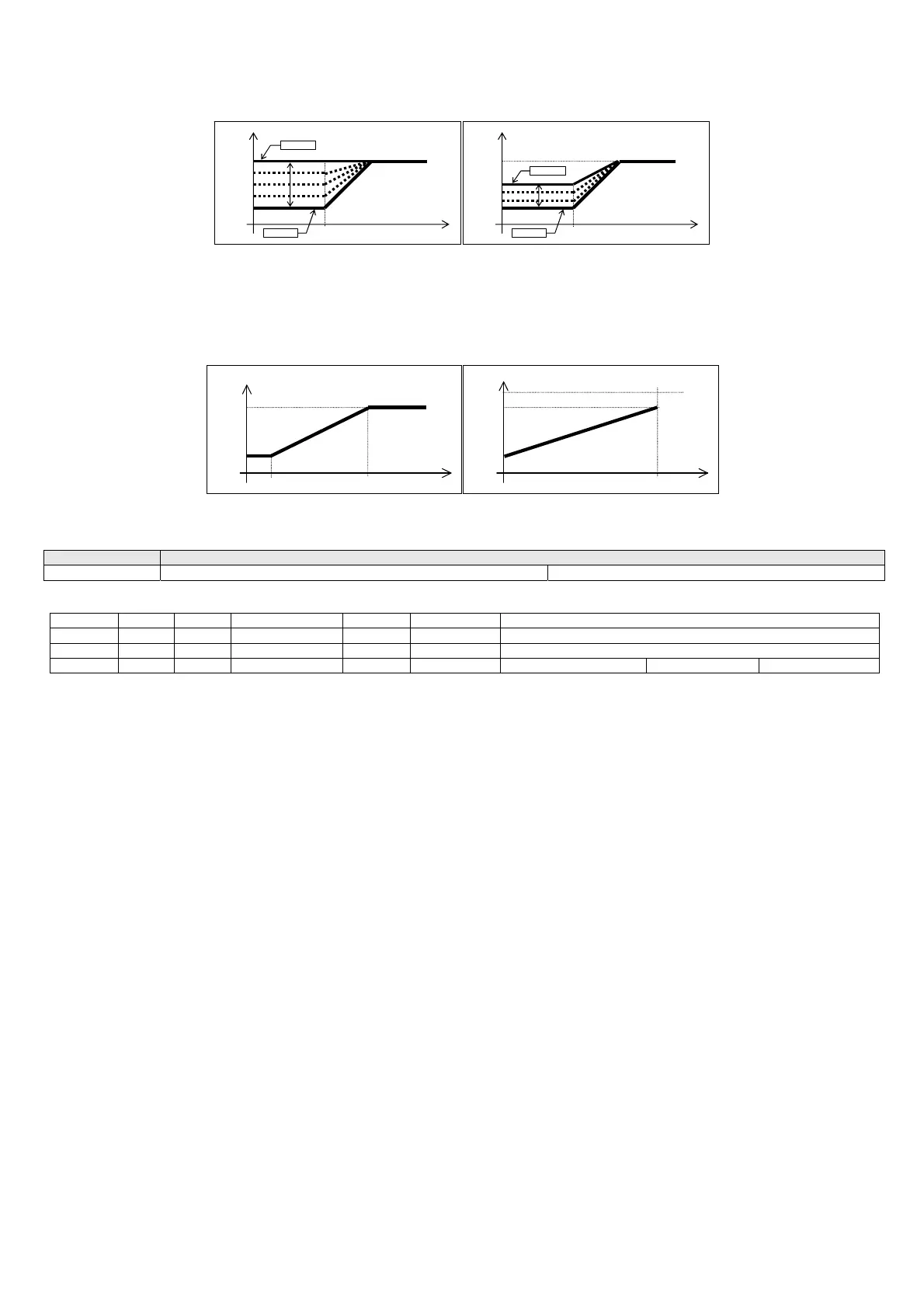
The maximum value of the reference outside temperature and the intensity of compensation (gain of the feedforward function) can be set by parameter (default 50°C
and 50% respectively).
The outside temperature below which the compensation function is deactivated is 0°C.
OUT
Feedforward 100%
max
min
setp
100%
100%
Text=max
Text=0°C
OUT
Feedforward 50
max
min
setp
100%
100%
Text=max
Text=0°C
(max+min)/2
Fig. 6.d
In the event of faults on probe B3, the controller considers the worst case scenario, that is, the maximum outside temperature. When set by trimmer, the MIN trimmer
is no longer used to set the minimum output (the minimum output value is taken from the parameter), but rather is used to set the gain for the feedforward function.
The effective minimum output calculated varies proportionally to the temperature read by probe B3, between the minimum value set by parameter and a maximum
value taken from the formula:
OUTminH = ( (OUTmax – OUTmin) x KFF/100 ) + OUTmin
OUTmin Feedforward
OUTminH
OUTmin
0
tB3 (°C)
OUTmax
OUTmin
0%
KFF
100%
TFF
OUTminH
100%
Fig. 6.e
The function is enabled when probe B3 is enabled. By default probe B3 is disabled and consequently so is the function.
Trimmer function
MIN Feedforward gain setting 0 to 100%
Table 6.a.s
Associated parameters
MIN I8 108 0 to MAX 30 1% Minimum output
KFF I14 114 0 to 100 50 1% Feedforward function gain
TFF A1 1 0.0 to +100.0 +50.0 0.1°C Max. reference outside temperature for feedforward function
PB3E D8 8 0/1 0 1 Enable probe B3 0=disabled 1=enabled
Table 6.a.t
6.9 PI control (proportional and integral)
In addition to the normal contribution of proportional control, the output is also controlled using the integral time on the error (deviation between the value measured
and set point).
This is used to reduce the error to zero.
out = Kp*err + Ki*Integral(err)
where err=error, Kp=proportional gain, Ki=integral gain, Ti=integral time, given by:
err = (measure – set point)
Kp = (max – min)/diff
Ki = Kp/Ti
By definition the integral time is the time required, when the error if constant, for the integral part to have the same contribution as the proportional part. The integral
time can be set by parameter (default 10 minutes). The contribution of the integral part can be reduced so as to avoid the phenomenon of “wind-up” (default 50%),
however in this case the error will not be removed in steady operation. Special care is required when setting the Ti, as excessively short times (see the inertia of the
system) may lead to instability. For a more detailed explanation of integral control, see the documents available on control theory.
When integral control is enabled, the output have values that are higher than the minimum output even if the value measured is less than the set point. Specifically, if
the Cut-off function is enabled, the output is forced to zero only when the output decreases until reaching the minimum value set (which certainly occurs for values <
(Set point – Differential)).
 Loading...
Loading...