Applications 17–17
82501F~1.DOC TI-83 international English Bob Fedorisko Revised: 10/26/05 1:49 PM Printed: 10/27/05 3:04
PM Page 17 of 20
Find the area given B=6, and N=10, 100, 150, 1000, and 10000.
Compare your results with p6
2
(the area of a circle with radius
6), which is approximately 113.097.
7. Enter
B=6. To find the area A, move the cursor onto A, and
then press ƒ [
SOLVE]. Find A for N=10, then N=100,
then
N=150, then N=1000, and finally N=10000. Notice that
as
N gets large, the area A approaches pB
2
.
Now graph the equation to see visually how the area changes as
the number of sides gets large.
8. Press z. Select the default mode settings.
9. Press p. Set the viewing window.
Xmin=0 Ymin=0 Xres=1
Xmax=200 Ymax=150
Xscl=10 Yscl=10
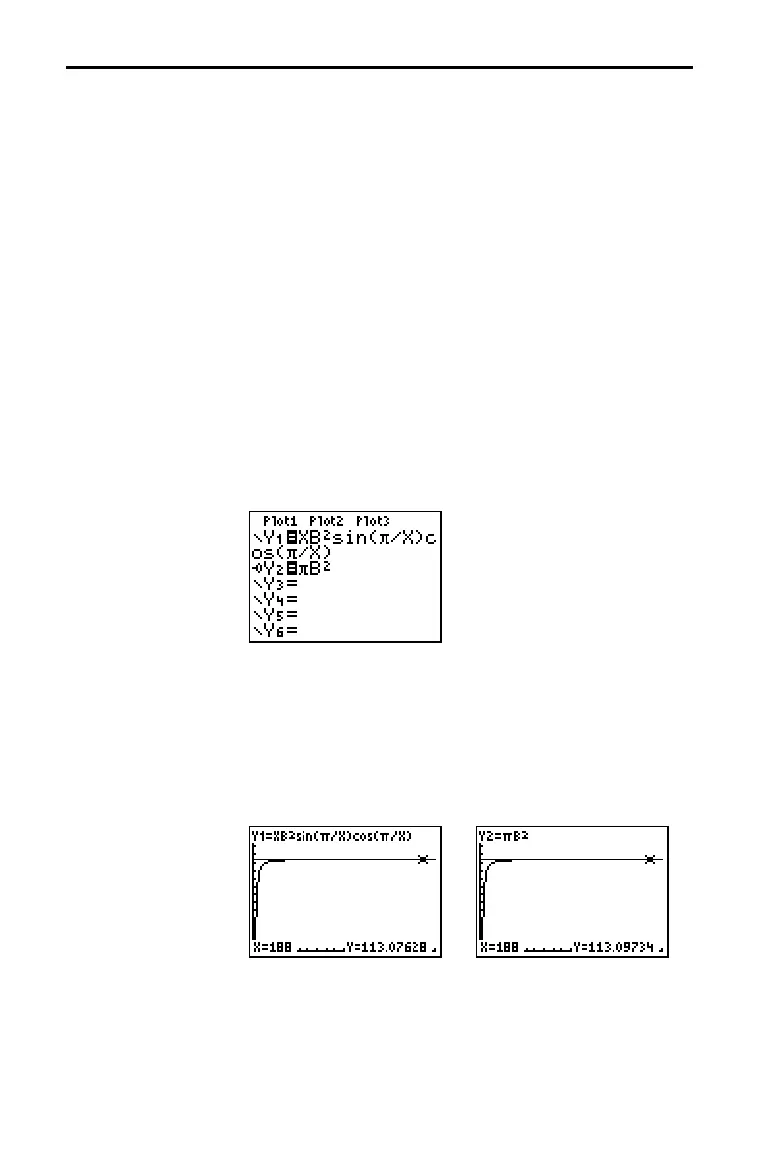
10.Press o. Turn off all functions and stat plots. Enter the
equation for the area. Use
X in place of N. Set the graph
styles as shown.
11.Press r. After the graph is plotted, press 100 Í to
trace to
X=100. Press 150 Í. Press 188 Í. Notice
that as
X increases, the value of Y converges to p6
2
, which is
approximately 113.097.
Y2=pB
2
(the area of the circle) is a
horizontal asymptote to
Y1. The area of an N-sided regular
polygon, with r as the distance from the center to a vertex,
approaches the area of a circle with radius r (pr
2
) as N gets
large.
Procedure
(continued)
To Next Page
Loading...
Need help?
General
