653
Double-precision Floating-point Instructions (CS1-H, CJ1-H, CJ1M, or CS1D Only) Section 3-16
Numbers Expressed as Floating-point Values
The following types of floating-point numbers can be used.
Note A non-normalized number is one whose absolute value is too small to be
expressed as a normalized number. Non-normalized numbers have fewer sig-
nificant digits. If the result of calculations is a non-normalized number (includ-
ing intermediate results), the number of significant digits will be reduced.
Normalized Numbers Normalized numbers express real numbers. The sign bit will be 0 for a positive
number and 1 for a negative number.
The exponent (e) will be expressed from 1 to 2,046, and the real exponent will
be 1,023 less, i.e., –1,022 to 1,023.
The mantissa (f) will be expressed from 0 to (2
52
– 1), and it is assumed that,
in the real mantissa, bit 2
52
is 1 and the decimal point follows immediately
after it.
Normalized numbers are expressed as follows:
(–1)
(sign s)
x 2
(exponent e)–1,023
x (1 + mantissa x 2
–52
)
Example
Sign: –
Exponent: 1,024 – 1,023 = 1
Mantissa: 1 + (2
51
+ 2
50
) x 2
–52
= 1 + (2
–1
+ 2
–2
) = 1 + (0.75) = 1.75
Value: –1.75 x 2
1
= –3.5
Non-normalized numbers Non-normalized numbers express real numbers with very small absolute val-
ues. The sign bit will be 0 for a positive number and 1 for a negative number.
The exponent (e) will be 0, and the real exponent will be –1,022.
The mantissa (f) will be expressed from 1 to (2
52
– 1), and it is assumed that,
in the real mantissa, bit 2
52
is 0 and the decimal point follows immediately
after it.
Non-normalized numbers are expressed as follows:
(–1)
(sign s)
x 2
–1,022
x (mantissa x 2
–52
)
Example
Sign: –
Exponent: –1,022
Mantissa: 0 + (2
51
+ 2
50
) x 2
–52
= 0 + (2
–1
+ 2
–2
) = 0 + (0.75) = 0.75
Value: –0.75 x 2
–1,022
= 1.668805 x 10
–308
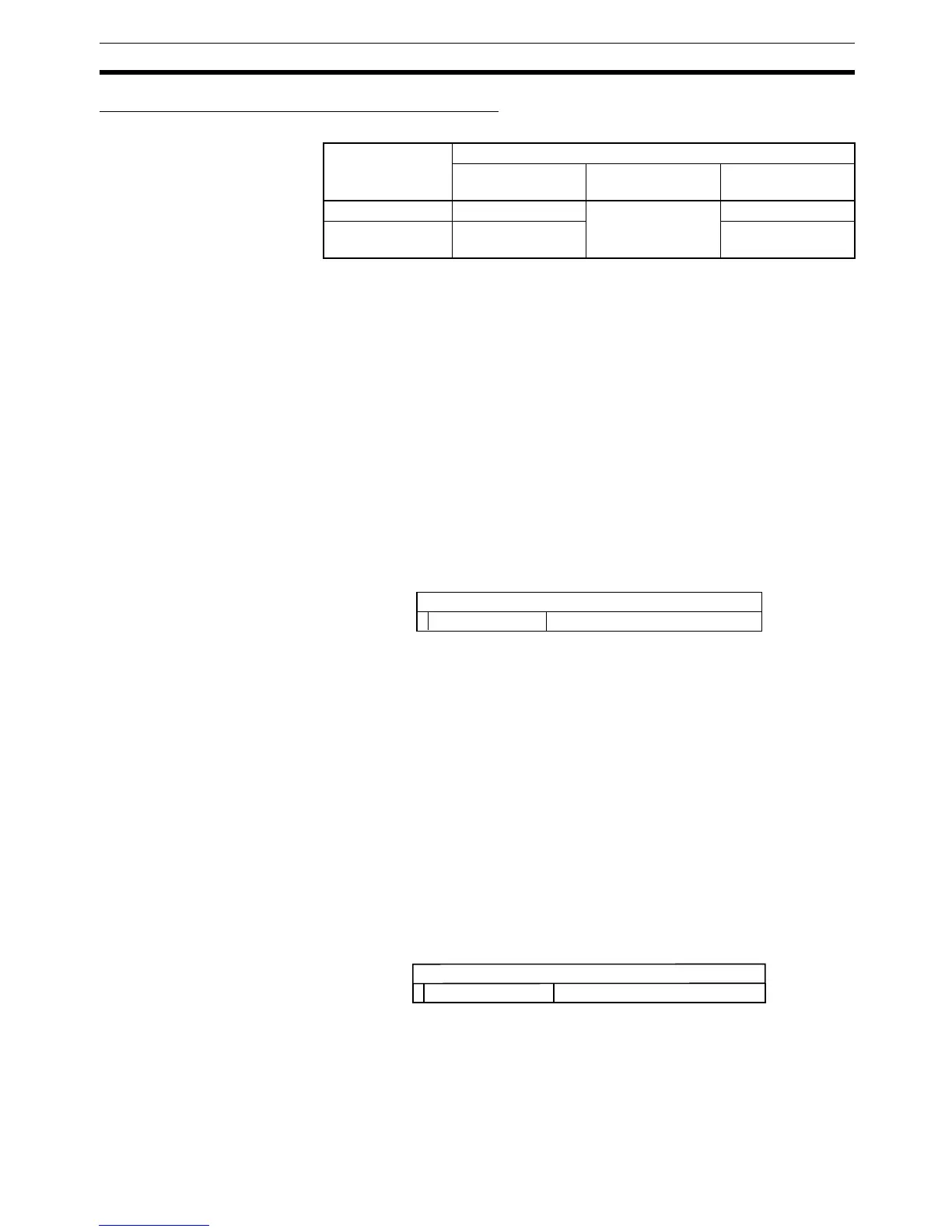
Mantissa (f) Exponent (e)
0 Not 0 and
not all 1’s (1,024)
All 1’s (1,024)
0 0 Normalized number Infinity
Not 0 Non-normalized
number
NaN
00000000000000000000000000000000
11000000000011000000000000000000
63 62 52 51
33
32
0
00000000000000000000000000000000
00000000000011000000000000000000
6463 5152
33
32
0

 Loading...
Loading...











