100 IF Z=2 THEN B=l: E=N-6: S=l
110 FOR P=B TO E STEP 7*S
120 PRINT "LOADING ROWS";P;"TO"; P+6*S
130 LPRINT CHR$(27)
"*"CHR$(5)CHR$(2*N)CHR$(0);
140 FOR C=N TO 1 STEP -1: GOSUB 180: NEXT C
150 FOR C=l TO N: GOSUB 180: NEXT C
160 LPRINT: NEXT P: NEXT Z
170 LPRINT CHR$(27)"@": END
180 F=0: FOR R=P TO P+6*S STEP S
190 IF A(R,C)=l THEN F=F+2^ABS(P+6*S-R)
200 NEXT R
220 LPRINT CHR$(F);: RETURN
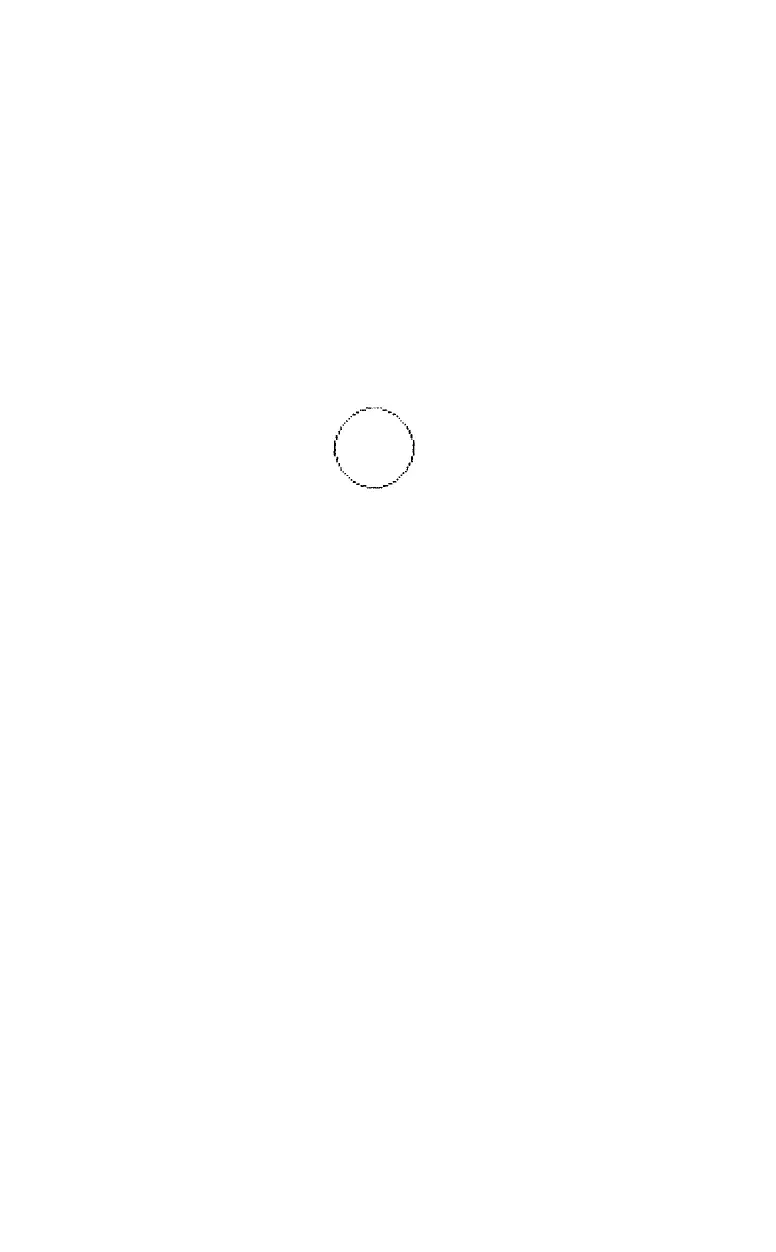
Go ahead and RUN it to see how it works.
There are two important points here:
1)
instead of tracing the circle
like a plotter,
the
program gathers the pattern in
the
computer’s mem-
ory, then prints it line by line; 2) the program takes advantage of
symmetry to print a figure four times the size of
the
original array.
Exploding galaxy
With a few more program changes, you can turn this mundane
circle into a design for an exploding galaxy. First change the size so
that
you can see the full impact of the figure (note that
105
is a multiple
of seven):
10 DEFINT A: N=l05: DIM A(N,N)
Yes, that 105 means this will take even longer to print out than
the circle did, but that’s the price you pay for largeness.
If your computer system requires a WIDTH statement to prevent
the printer from issuing a carriage return before the graphics line is
complete, add it now:
7 WIDTH LPRINT 255
The format for this statement may be different for your BASIC; see
your software documentation.
Next modify the distance formula slightly. Type:
30 D=SQR(R^2+C^2)/N: D=D*D
184
To Next Page
Loading...
Need help?
General
