Mitsubishi MELDAS HS Series User Manual

Chapter 11 Selection
11–14
11-6 Expressions for load inertia calculation
The calculation method for a representative load inertia is shown.
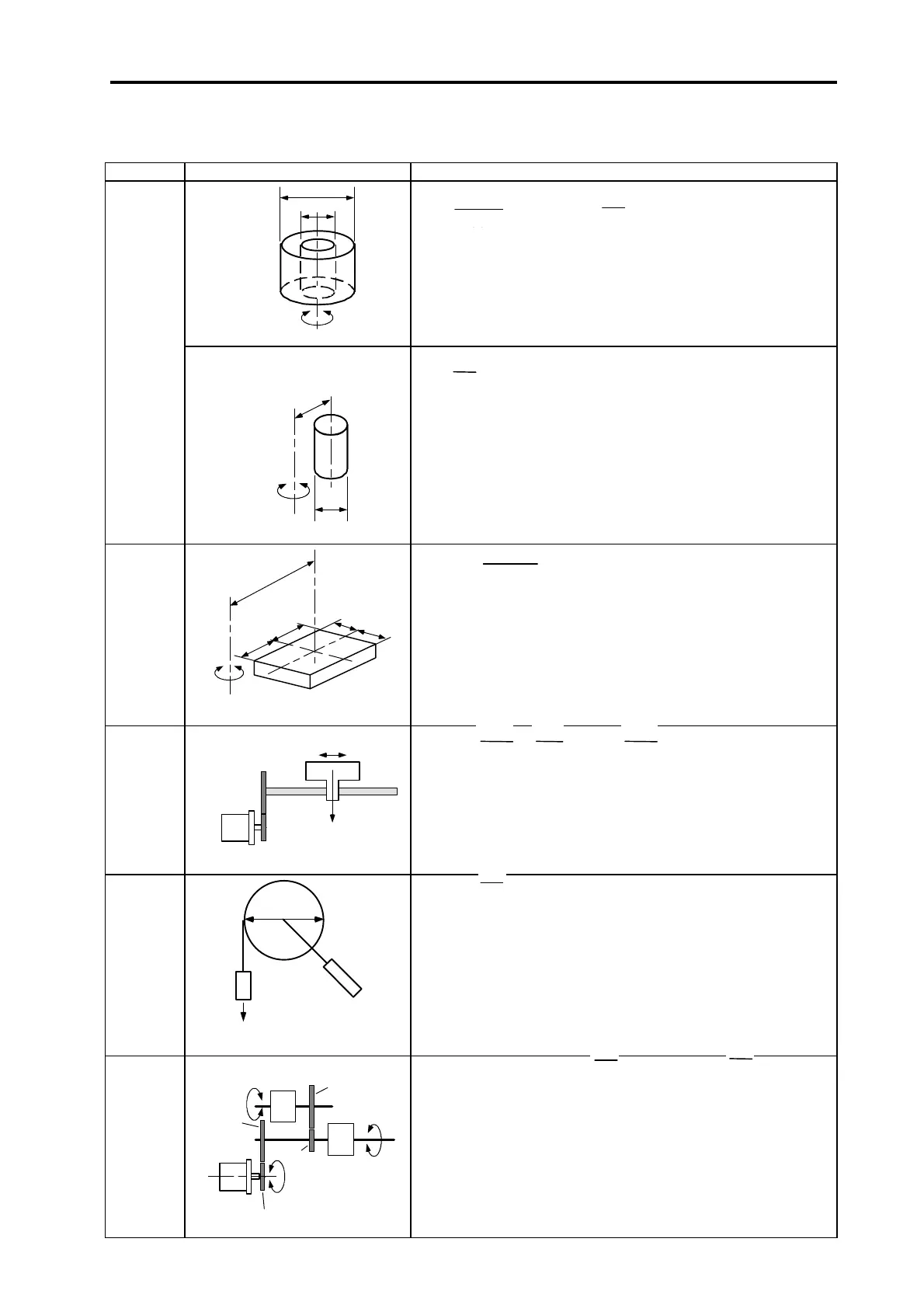
Type Mechanism Calculation expression
R
o
t
a
r
y

s
h
a
f
t
φD1.
φD
2.

JL = (D
1
4
– D
2
4
) = (D
1
2
– D
2
2
)
Cylinder
When rotary shaft and cylinder
shaft are deviated

D
R
o
t
a
r
y

s
h
a
f
t
R
JL = (D
2
+ 8R
2
)
Column
a
a
b
b
R
o
t
a
r
y

s
h
a
f
t
R
JL = W ( + R
2
)
Object that
moves
linearly
W
V
N
Servomotor
JL = W ( · )
2
= W ( )
2
Suspended
object
D
W
JL = W ( )
2
+ JP
Converted
load
Servomotor
LoadA
JA
N2
N1
N1
J
11
J21
J31
LoadB
JBN3
J22
JL = J
11
+ (J
21
+ J
22
+ J
A
) · ( )
2
+ (J
31
+ J
B
) · ( )
2
W
8
N
3
N
1
N
2
N
1
π · ρ
·L
32
W
8
a
2
+ b
2
8
JL : Load inertia
[kg·m
2
]
W : Weight of object that moves linearly [kg]
N : Motor speed
[r/min]
V : Speed of object that moves linearly [mm/min]
V
10
1
2πN
△S
20π
JL : Load inertia [kg·m
2
]
W : Weight of cylinder [kg]
D : Outer diameter of cylinder [m]
R : Distance between rotary axis and
cylinder axis [m]
JL : Load inertia [kg·m
2
]
W : Weight of cylinder [kg]
a.b.R : Left diagram [m]
D
2
JL : Load inertia [kg·m
2
]
W : Weighty of object [kg]
D : Diameter of pulley [m]
JP : Inertia of pulley [kg·m
2
]
JL : Load inertia [kg·m
2
]
JA,JB : Inertia of load A, B [kg·m
2
]
J
11
~J
31
: Inertia [kg·m
2
]
N
1
~N
3
: Each shaft’s speed [r/min]
JL : Load inertia [kg·m
2
]
ρ : Density of cylinder
material[kg·m
3
]
L : Length of cylinder [m]
D
1
: Outer diameter of cylinder [m]
D
2
: Inner diameter of cylinder [m]
W : Weight of cylinder [kg]
Reference data
Material densities Iron
..... 7.80×10
3
[kg/m
3
]
Aluminum
..... 2.70×10
3
[kg/m
3
]
Copper
..... 8.96×10
3
[kg/m
3
]
Rotary
shaft is
cylinder
center

Mitsubishi MELDAS HS Series Specifications

General

Brand	Mitsubishi
Model	MELDAS HS Series
Category	Servo Drives
Language	English