TI-83, TI-83 Plus, TI-84 Plus Guide
Return to the home screen. The matrix that holds the solution
to the system of equations, provided a solution exists, is
obtained with
1
2ND (MATRIX)x
−
1 [A]
1
1
2ND (MATRIX)x
−
2 [B] ENTER .
NOTE: Carefully notice the order in which you entered the coefficients. Because the coef-
ficient of l was input first in matrix A, the first value in the solution is l. The other value is t.
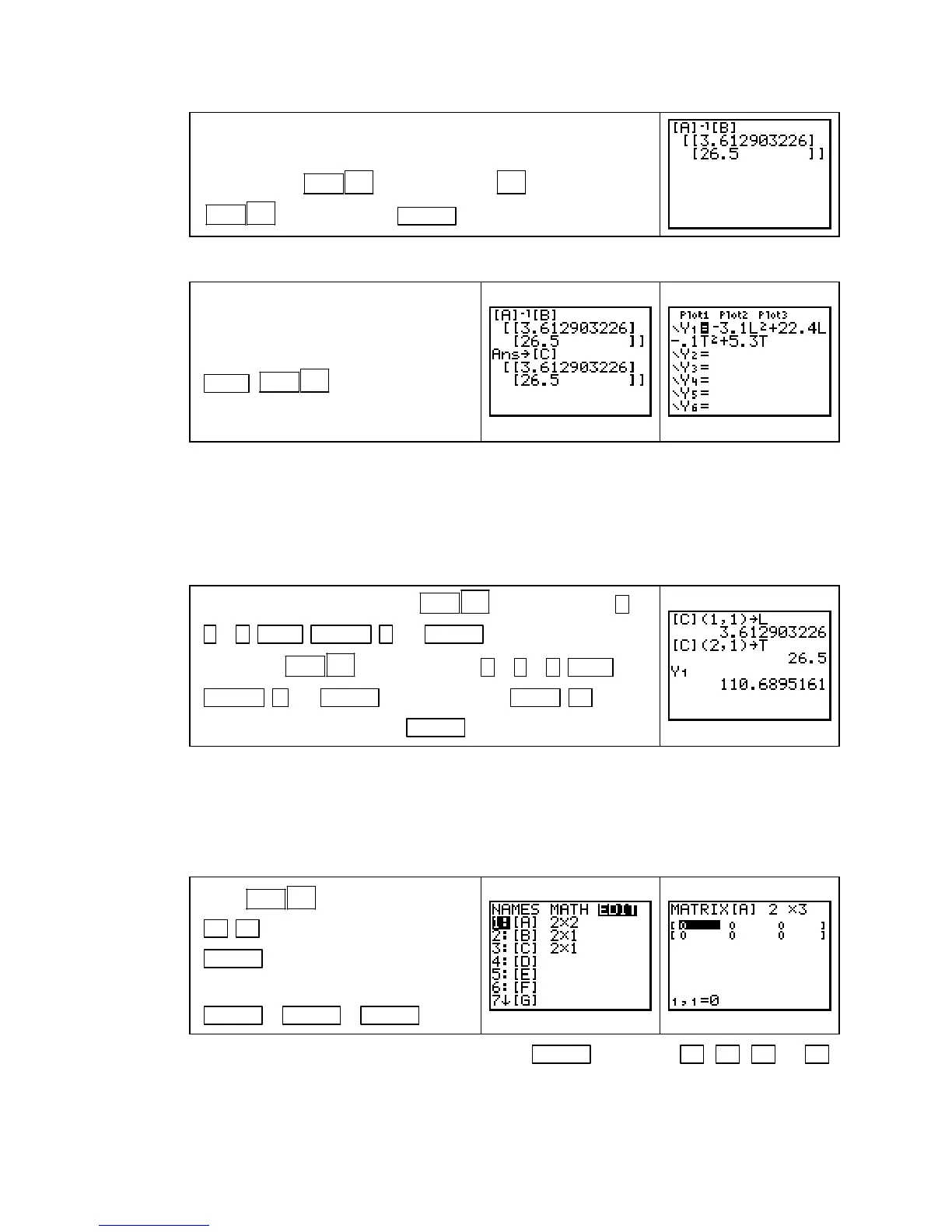
We need to use these unrounded values
to find the multivariable function out-
put at the critical point. So, store this
solution in another matrix, say
C, with
STO`
1
2ND (MATRIX)x
−
3 [C].
Also, enter the multivariable function V
in
Y1.
We have found that l ≈ 3.61 grams and t = 26.5 minutes. We show how to recall a particular
matrix element so that we can use the unrounded values of l and t to find the multivariable
function output. Recall that matrix elements are referred to by the row and then the column in
which they appear. Because
C is a 2 by 1 matrix (2 rows and 1 column) and we set up the
equations so that l was the input variable whose coefficient we entered first in matrix
A, l is in
the (1, 1) position and t is in the (2, 1) position.
Store the value of l into L with
1
2ND (MATRIX)x
−
3 [C] ( 1
,
1 ) STO` ALPHA ) (L) ENTER . Store the value of t
into
T with
1
2ND (MATRIX)x
−
3 [C] ( 2 , 1 ) STO`
ALPHA
4 (T) ENTER . Find V(l, t) with VARS ►
[Y−VARS] 1 [Function] 1 [Y1] ENTER .
Method 2: Using a Single Matrix
We choose to use A as the single matrix. The cake volume index system of equations contains
2 input variables, a constant term in each equation, and 2 equations, so we set the dimension of
A to 2 by 3; that is, A will have 2 rows and 3 columns. (Your calculator screens corresponding
to the screens shown in the first box below may have numbers different from those indicated.)
Press
1
2ND (MATRIX)x
−
and then
► ► to go to the EDIT menu. Press
ENTER .
Change the dimension of
A by pressing
ENTER 2 ENTER 3 ENTER .
NOTE: You can move around the matrix with ENTER or by using ► , ◄ , ▲ , or ▼ .
Copyright © Houghton Mifflin Company. All rights reserved.
109
To Next Page
Loading...
Need help?
General
