TI-83, TI-83 Plus, TI-84 Plus Guide
3a. Clear
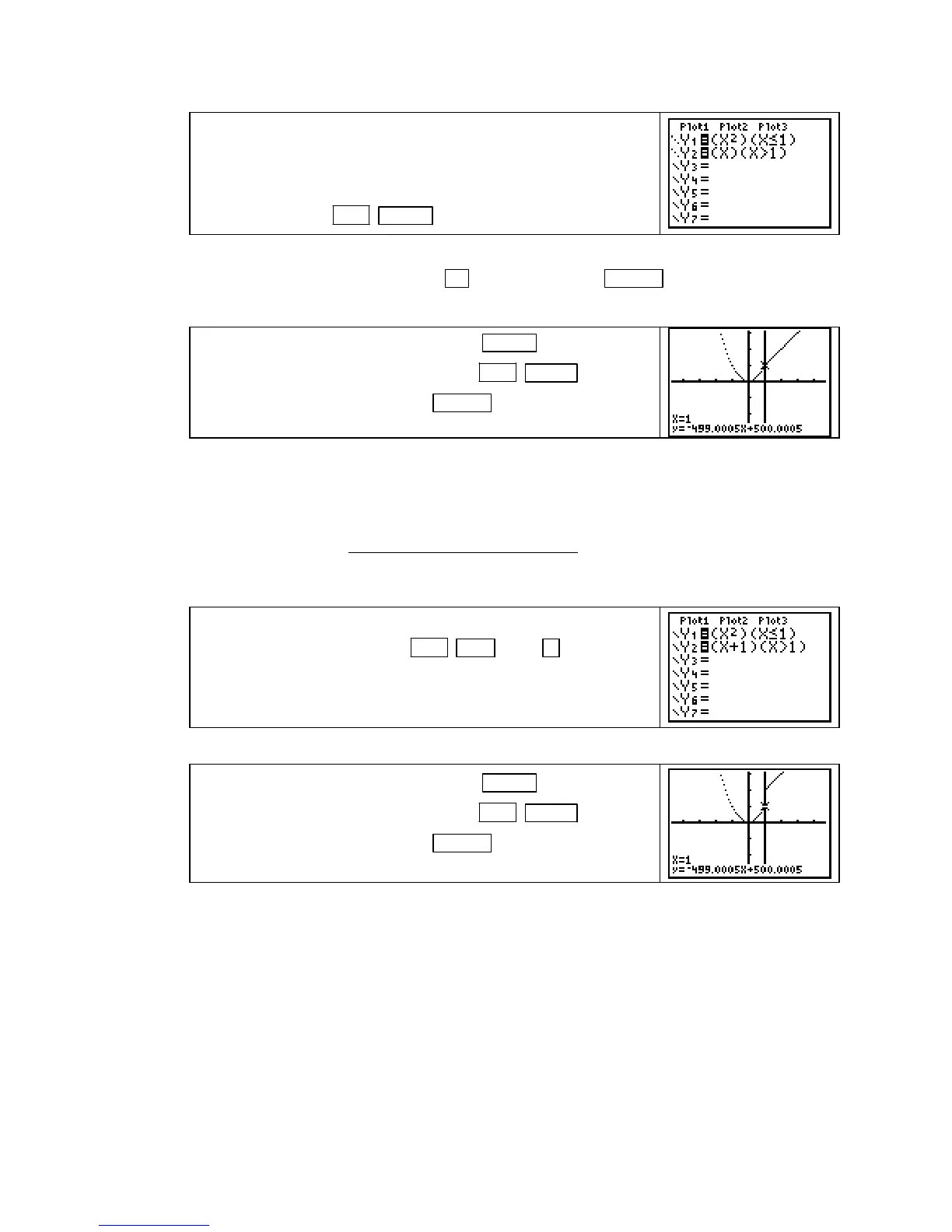
Y1 and Y2 and enter, as indicated, the function
. (The inequality symbols are
accessed with
hx
xx
xx
()
when
when
=
≤
>
R
S
|
T
|
2
1
1
2ND MATH (TEST).
Set each part of the function to draw in DOT mode by placing the cursor over the equals
sign in each function, pressing
◄ , and then pressing ENTER 6 times until the slanted
line turns to a dotted line.
Draw the graph of the function with ZOOM 4 [ZDecimal].
With the graph on the screen, press 2ND PRGM (DRAW)
5 [Tangent(],
then press 1 and ENTER . The tangent line is
drawn at the break point,
x = 1.
THE GRAPH YOU SEE IS INCORRECT. Even though h is continuous for all values
of x, there is no tangent line to the graph of h at x = 1. Secant lines drawn using close
points on the right and on the left of x = 1 do not approach the same slope, so the
instantaneous rate of change of h does not exist at x = 1.
NOTE: There is no tangent line at the break point of a piecewise continuous function
(even if that function is continuous at the break point) unless secant lines drawn through
close points to the left and right of that point approach the same value.
3b. Edit Y2 by placing the cursor over the right parenthesis
following
X and pressing 2ND DEL (INS) + 1 to enter
mx
xx
xx
()
when
when
=
≤
+>
R
S
|
T
|
2
1
11
The calculator should still be in DOT mode from the previous graph.
Draw the graph of the function with ZOOM 4 [ZDecimal].
With the graph on the screen, press 2ND PRGM (DRAW)
5 [Tangent(],
then press 1 and ENTER . The tangent line is
drawn at the break point,
x = 1.
CAUTION: THE GRAPH YOU SEE IS INCORRECT. Because m is not continuous
when x = 1, the instantaneous rate of change does not exist at that point. The tangent
line cannot be drawn on the graph of m when x = 1. Be certain that the instantaneous rate
of change exists at a point and the tangent line exists at that point before using your
calculator to draw a tangent line or use the tangent equation that may be printed on the
screen. Because of the method that your calculator uses to compute instantaneous rates
of change, it might draw a tangent line at a point on a curve where the tangent line,
according to our definition, does not exist.
Copyright © Houghton Mifflin Company. All rights reserved.
49

 Loading...
Loading...

















