Chapter 5
We next find the inputs of the points of intersection of the two functions. (These values will
probably be the limits on the integrals we use to find the areas.) The method we use to find the
first of the points is the intersection method that was discussed on page A-11 of this Guide.
With the graph on the screen, press
2nd TRACE (CALC) 5
[intersect].
The calculator asks FIRST CURVE? Press ENTER
to mark Y1. The calculator then asks SECOND CURVE? Press
ENTER to mark Y2. At the GUESS? prompt, use ◄ to move
the cursor near the leftmost visible point of intersection.
Press ENTER to find t ≈ 3.724. To avoid making a mistake
copying this value and to eliminate as much rounding error as
possible, return to the home screen and store the input value in
A with the keystrokes
X,T,θ,n STO` ALPHA MATH (A).
You could use this same method to find B, the input value of the
rightmost point of intersection. However, to illustrate another
way this can be done, we find this value using the
SOLVER. The
equation we are solving is
Y1 = Y2, but remember that what you
enter in the
SOLVER must have 0 on one side of the equation.
Access the SOLVER with MATH 0. Press ▲ CLEAR and
enter the equation Y1 − Y2. Note from the graph that B is near 14.
Use this or some other value closer to B than it is to A as your
guess. Press
ALPHA ENTER (SOLVE) to find that B ≈ 14.242.
As with the first point, to avoid making a mistake copying this
input value and to eliminate as much rounding error as possible,
return to the home screen and store this value in B with the
keystrokes
X,T,θ,n STO` ALPHA MATRX (B).
NOTE: Even though we have found the only intersection points that are useful in the context
of this example, the
SOLVER can easily find if there are any other intersection points for these
two curves. Enter several different guesses, some smaller than A and some larger than B. (We
can see from the graph that there are no other points of intersection between A and B.) You
should find that these curves also intersect at t
≈
−
0.372 and t ≈ 27.97
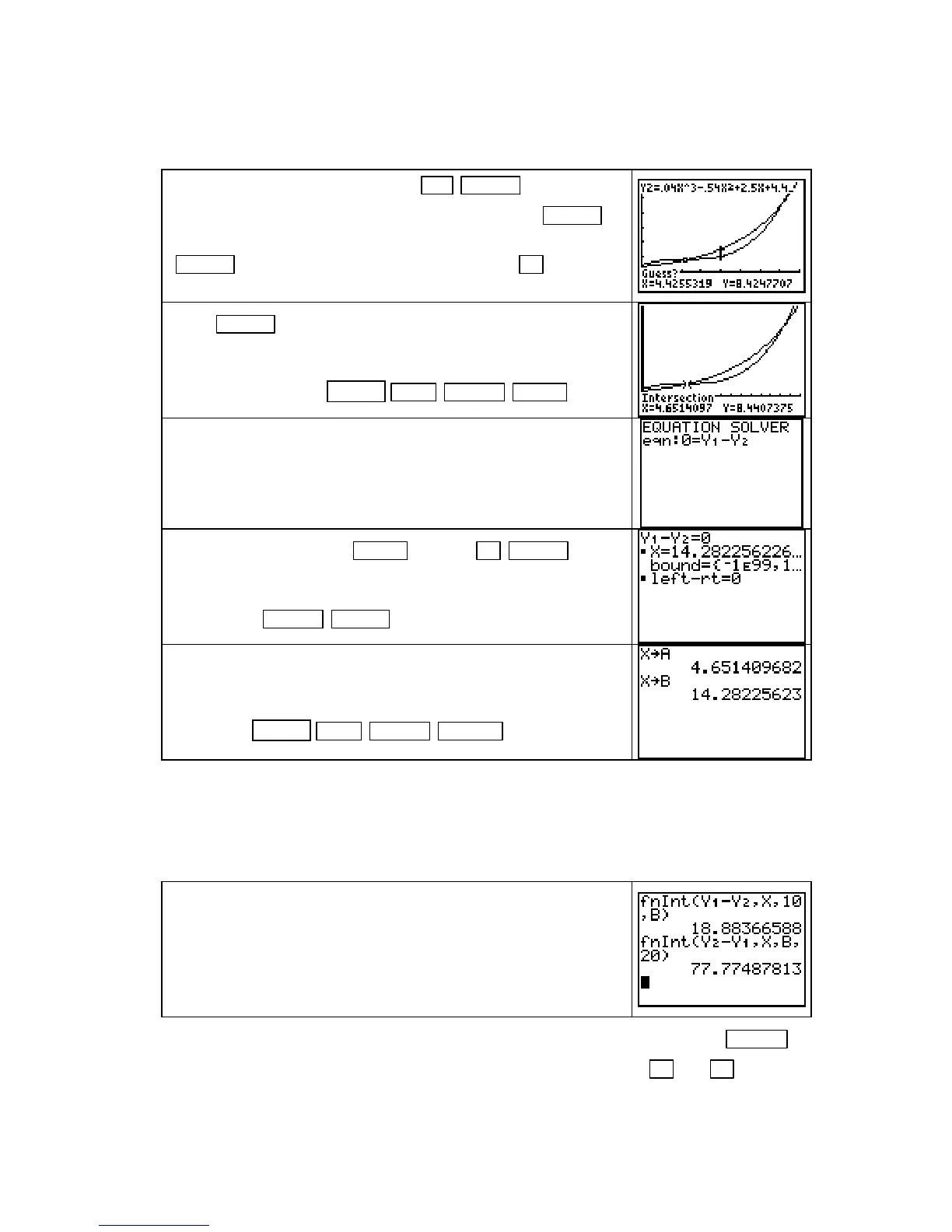
Calculate the areas of the two regions enclosed by s and a (that
is, regions
R
1
and R
2
that are shown in Figure 5.5 in the text) as
indicated to the right.
Note that each answer should be positive because we are finding
areas. If you obtain a negative answer, you probably entered the
functions in the wrong order.
If you are in doubt as to which function to enter first in the integral, you can press GRAPH
and trace the graphs to see which function is on top of the other. Press ▲ and ▼ to have
the cursor jump from one curve to the other and notice the equation at the top of the screen.
Copyright © Houghton Mifflin Company. All rights reserved.
78

 Loading...
Loading...

















