7.1 Selecting Motors and Inverters
7-7
Chap. 7 SELECTING OPTIMAL MOTOR AND INVERTER CAPACITIES
7.1.3 Equations for selections
7.1.3.1 Load torque during constant speed running
[ 1 ] General equation
The frictional force acting on a horizontally moved load must be calculated. Calculation for driving a load
along a straight line with the motor is shown below.
Where the force to move a load linearly at constant speed X(m/s) is F (N) and the motor speed for driving
this is N
M (r/min), the required motor output torque W
M
(N·m) is as follows:
)mN(
Ș
F
N
ʌ2
ȣ60
8507.8
G
M
M
IJ
xx
x
x
u
(7.1)
where, K
G
is Reduction-gear efficiency.
When the inverter brakes the motor, efficiency works inversely, so the required motor torque should be
calculated as follows:
)mN(ȘF
N
ʌ2
ȣ60
8507.8
G
M
M
IJ
xxx
x
x
u
(7.2)
(60·X) / (2S·N
M
) in the above equation is an equivalent turning radius corresponding to speed Xaround the
motor shaft.
The value F (N) in the above equations depends on the load type.
[ 2 ] Obtaining the required force F
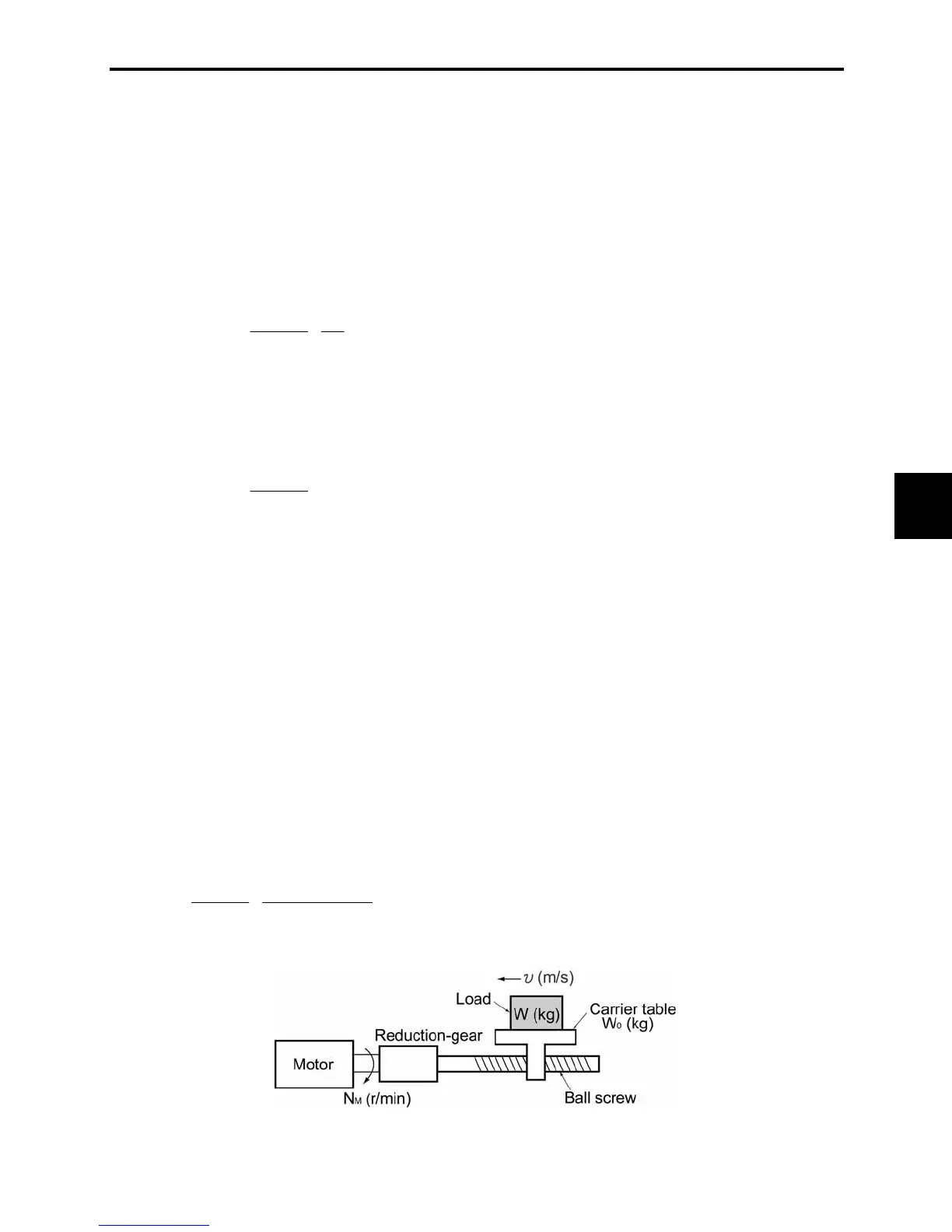
Moving a load horizontally
A simplified mechanical configuration is assumed as shown in Figure 7.7. If the mass of the carrier table is
W
0
kg, the load is W kg, and the friction coefficient of the ball screw is P, then the friction force F (N) is
expressed as follows, which is equal to a required force for driving the load:
)N(g)WW(F
0
xx
(7.3)
where, g is the gravity acceleration (| 9.8 m/s
2
).
Then, the required output torque around the motor shaft is expressed as follows:
)mN(
Ș
μg)WW(
N
ʌ2
ȣ60
G
0
M
M
IJ
x
xx
x
x
x
(7.4)
Figure 7.7 Moving a Load Horizontally
To Next Page
Loading...
Need help?
General
