3-210 Full Command and Function Reference
See also: APPLY, QUOTE
√ (Square Root)
Type: Function
Description: Square Root Analytic Function: Returns the (positive) square root of the argument.
For a complex number (x
1
, y
1
), the square root is this complex number:
x
2
y
2
,() r
θ
2
---
r,cos
θ
2
---sin
⎝⎠
⎛⎞
=
where r = ABS (x
1
, y
1
), and θ = ARG (x
1
, y
1
).
If (x
1
, y
1
) = (0,0), then the square root is (0, 0).
The inverse of SQ is a relation, not a function, since SQ sends more than one argument to the same
result. The inverse relation for SQ is expressed by ISOL as this general solution:
's1*√Z'
The function √ is the inverse of a part of SQ, a part defined by restricting the domain of SQ such that:
1. each argument is sent to a distinct result, and
2. each possible result is achieved. The points in this restricted domain of SQ are called the principal
values of the inverse relation. The √ function in its entirety is called the principal branch of the inverse
relation, and the points sent by √ to the boundary of the restricted domain of SQ form the branch
cuts of √.
The principal branch used by the hp49g+/hp48gII for √ was chosen because it is analytic in the
regions where the arguments of the real-valued inverse function are defined. The branch cut for the
complex-valued square root function occurs where the corresponding real-valued function is
undefined. The principal branch also preserves most of the important symmetries.
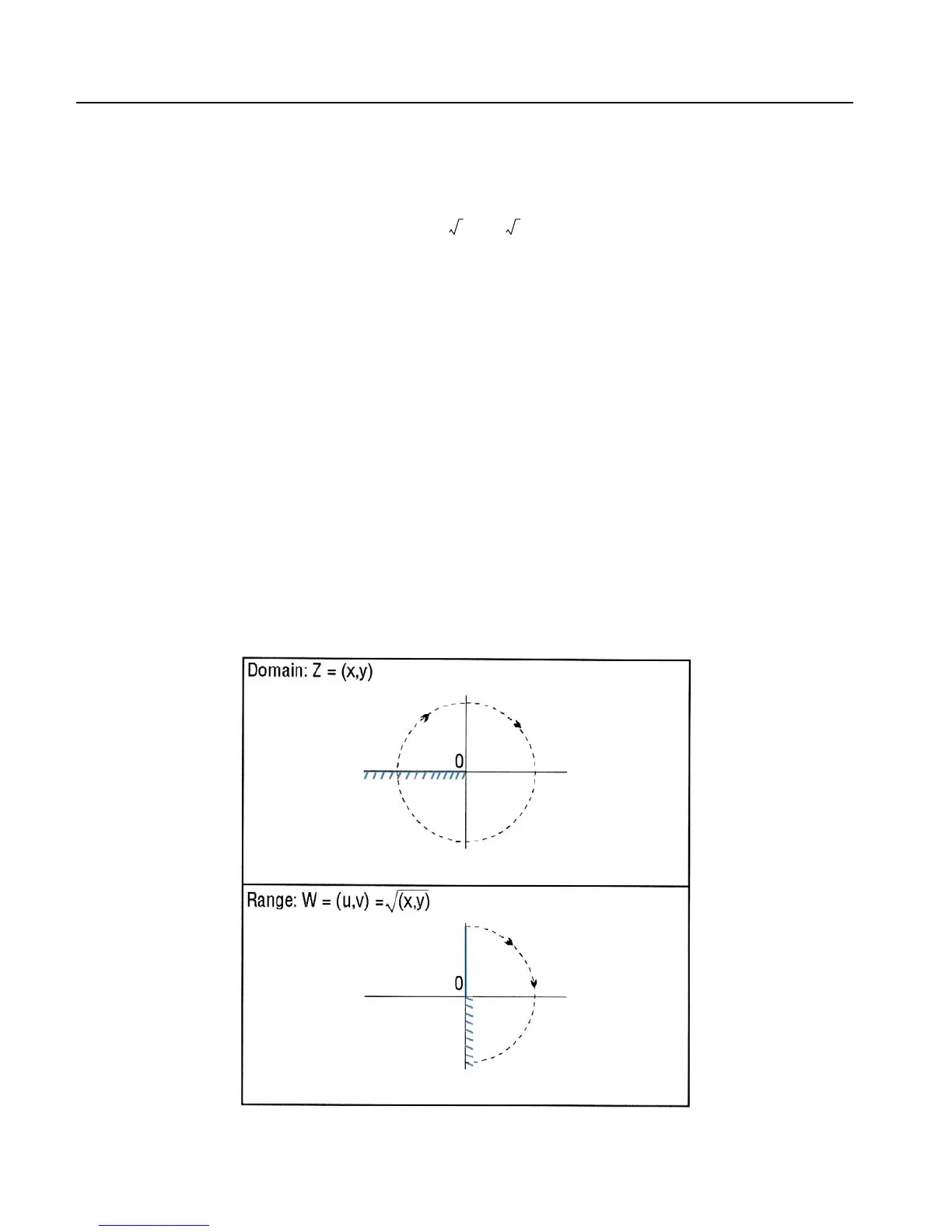
The graphs below show the domain and range of √. The graph of the domain shows where the
branch cut occurs: the heavy solid line marks one side of the cut, while the feathered lines mark the
other side of the cut. The graph of the range shows where each side of the cut is mapped under the
function.
To Next Page
Loading...
Need help?
General
Weight and Dimensions
