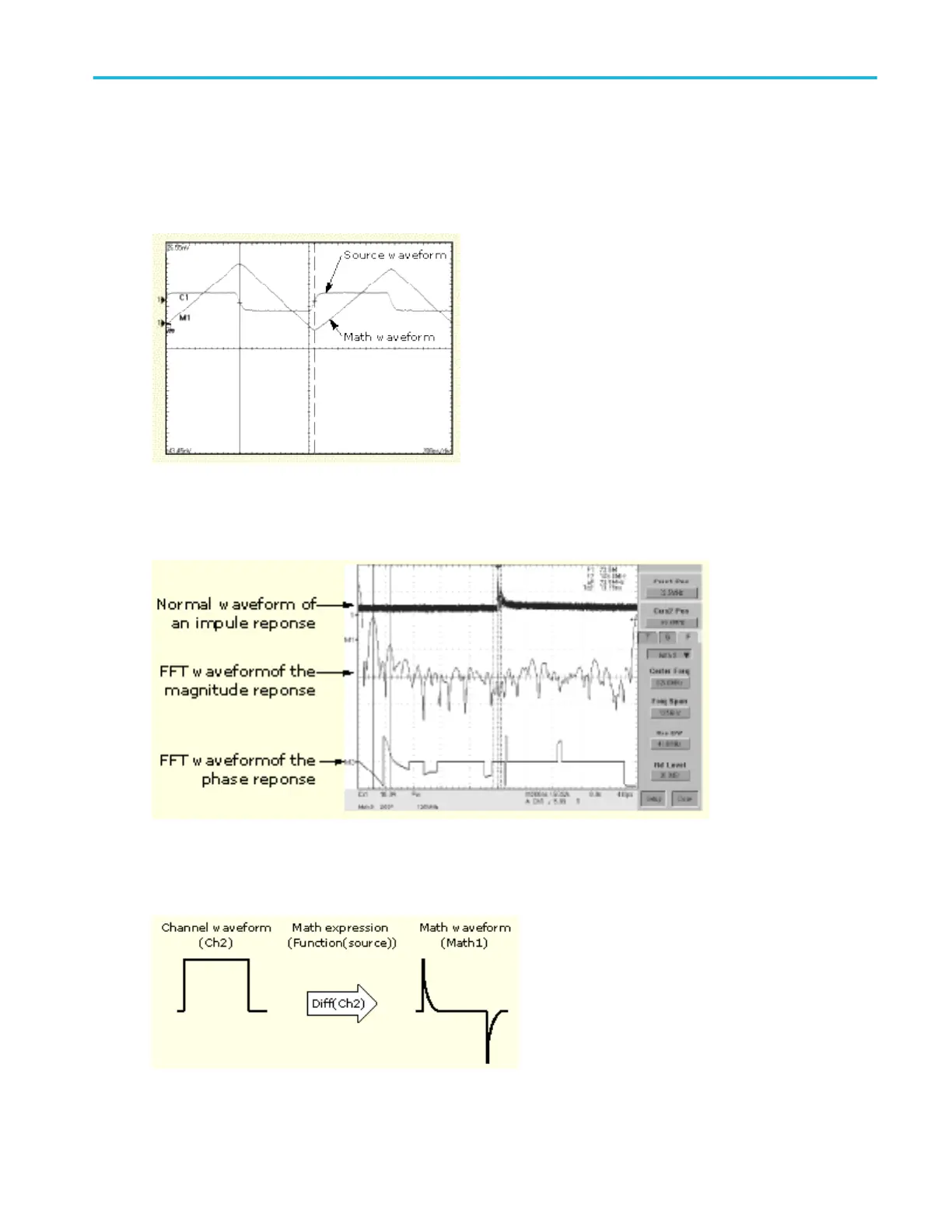
Math waveforms
Once you have acquired waveforms or taken measurements on waveforms, the instrument can mathematically combine them to
create a waveform that supports your data-analysis task. For example, you might have a waveform clouded by background
noise. You can obtain a cleaner waveform by subtracting the background noise from your original waveform. Or, you can
integrate a single waveform into an integral math waveform as shown below.
With spectral analysis you can analyze waveforms in the frequency domain. The interface is similar to a dedicated spectrum
analyzer, so you do not need to know the details of the underlying algorithms. See the next figure.
This instrument supports mathematical combination and functional transformations of waveforms it acquires. The next figure
shows this concept:
Oscilloscope reference
DPO70000SX, MSO/DPO70000DX, MSO/DPO70000C, DPO7000C, and MSO/DPO5000B Series 703
To Next Page
Loading...
Need help?
General
