277
T
T
h
h
e
e
‘
‘
P
P
o
o
l
l
y
y
n
n
o
o
m
m
i
i
a
a
l
l
’
’
g
g
r
r
o
o
u
u
p
p
o
o
f
f
f
f
u
u
n
n
c
c
t
t
i
i
o
o
n
n
s
s
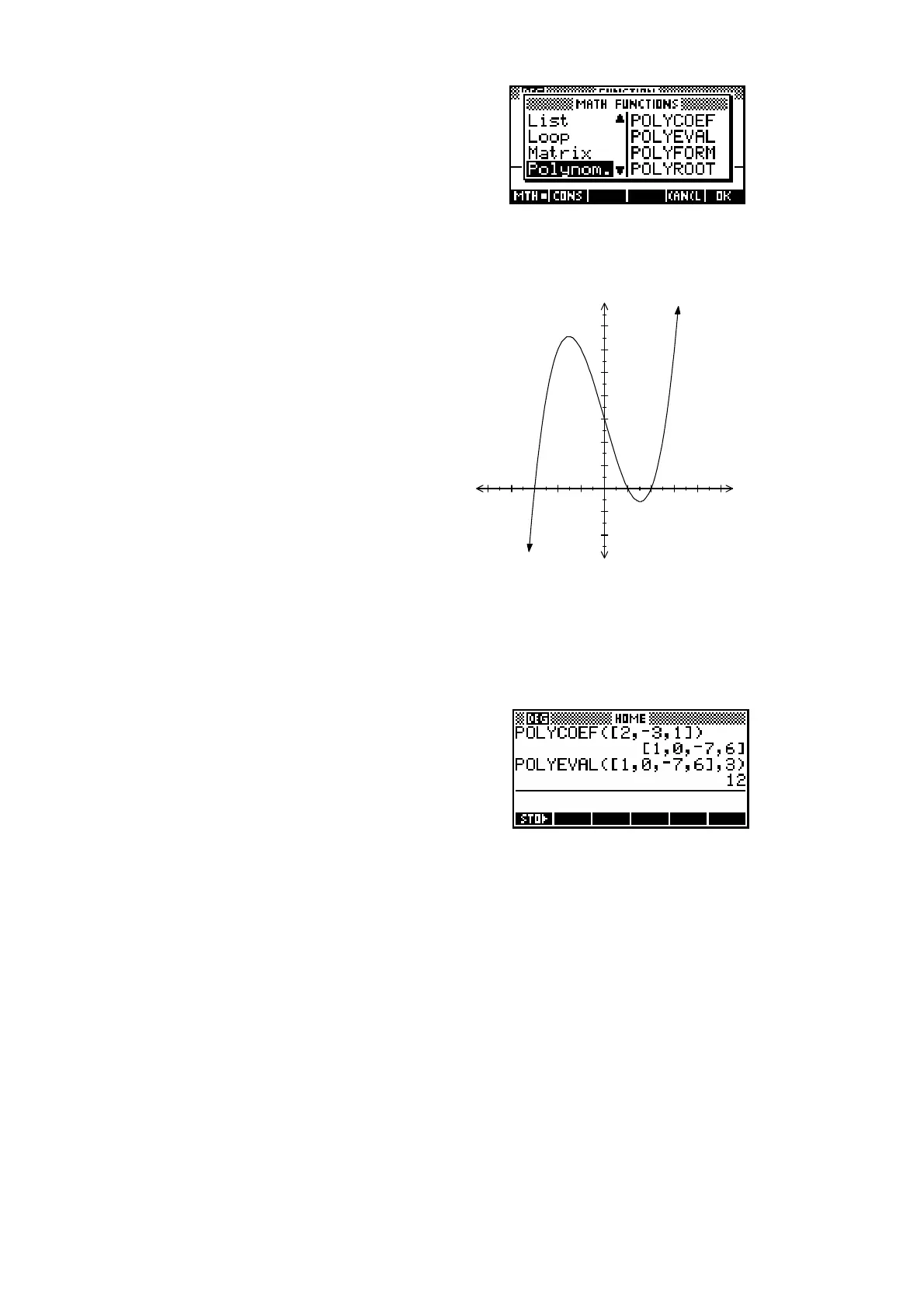
This group of functions is provided to manipulate polynomials.
We will use the following function to illustrate some of the tools in the
Polynomial group.
3
() ( 2)( 3)( 1) 7 6fx x x x x x=− + −=−+
POLYCOEF([root1,root2,…])
This function returns the coefficients of a polynomial with roots
123
, , ,...xxx
The roots must be supplied in vector form means in square brackets.
The function
()
x
above has roots 2, -3 and 1. The screen shot below
shows POLYCOEF correctly giving the coefficients as 1, 0, -7 and 6 for a
final polynomial of
3
() 7 6fx x x=−+.
POLYEVAL([coeff1,coeff2,…],value)
This function evaluates a polynomial with specified coefficients at the point
specified. The coefficients must be in square brackets, followed by the value
of x (not in brackets). ie.
()
3
76
xx x=−+ has value 12 at x = 3.
Note: If evaluating more than one point it is probably more efficient to enter
the function into the SYMB view of the Function aplet. Then either use
the NUM view to find the function values required, or simply type F1(3),
F1(-2) etc. in the HOME view.
f(x)
1 2 3 4 5-1-2-3-4-5
2
4
6
8
10
12
14
-2
-4
To Next Page
Loading...
Need help?
General
