HP 39G Master Guide

294
I
I
n
n
c
c
o
o
n
n
s
s
i
i
s
s
t
t
e
e
n
n
t
t
s
s
y
y
s
s
t
t
e
e
m
m
s
s
o
o
f
f
e
e
q
q
u
u
a
a
t
t
i
i
o
o
n
n
s
s
Solve each of the systems of equations
below, where possible, indicating in
each case the nature of the system.
(a)
23 7
415
22
xz
xy z
xyz
−=−
++ =
+−=
(b)
23 7
415
38
xz
xy z
xyz
−
=−
++ =
++=
(c)
23 7
415
37
xz
xy z
xyz
−
=−
++ =
++=
Using the RREF function
In each case the most efficient method
is to use the function RREF. The letters
RREF stand for Reduced Row Echelon
Form and the advantage of this function is that
it allows the user to deal with matrices which
are singular.
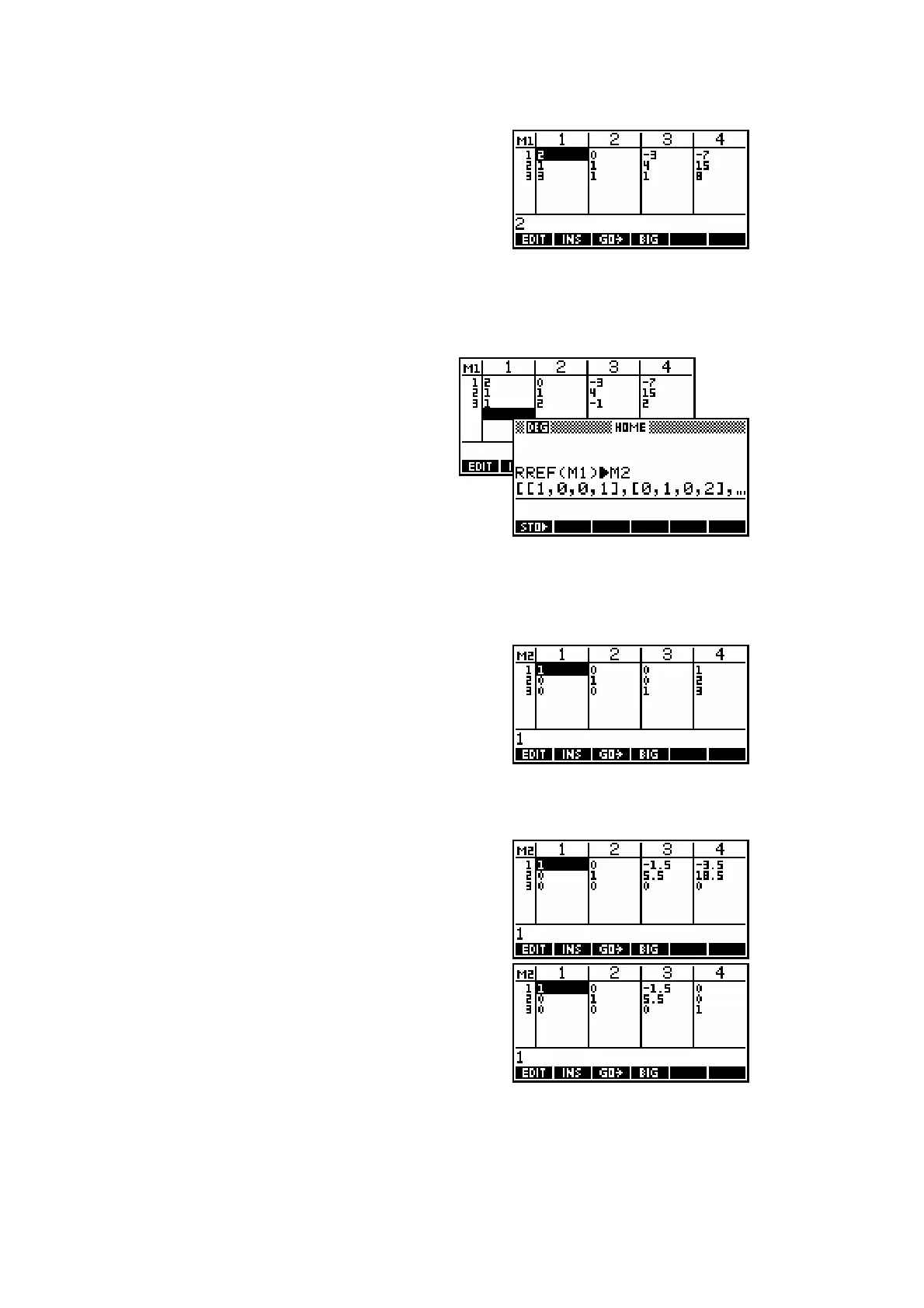
(a) Entering the augmented matrix of coefficients into M1 (see above) we
then use the RREF function, storing the result into M2.
This result can be examined via the
Matrix Catalog. It can be seen that
the result is a diagonal of 1
s, with the
result given in the final column.
Here: x = 1, y = 2, z = 3
(b) Since the coefficients are similar, we can edit the augmented matrix in
M1 and then re-use the line in the HOME view.
In this case the final line of zeros
indicates that the original matrix is
singular and that there are an infinite
number of valid solutions.
(c) A similar method for the third set of
coefficients yields the result shown
right. The final line of 0 0 0 1
indicates that there is no valid solution.

HP 39G Specifications

General

Brand	HP
Model	39G
Category	Calculator
Language	English