10.1 Selecting Motors and Inverters
10-9
Chapter 10 SELECTING OPTIMAL MOTOR AND INVERTER CAPACITIES
[2] Acceleration and deceleration time calculation
When an object whose moment of inertia is J (kg·m
2
) rotates at the speed N (r/min), it has the following
kinetic energy:
To accelerate the above rotational object, the kinetic energy will be increased; to decelerate the object, the
kinetic energy must be discharged. The torque required for acceleration and deceleration can be
expressed as follows:
This way, the mechanical moment of inertia is an important element in the acceleration and deceleration.
First, calculation method of moment of inertia is described, then those for acceleration and deceleration
time are explained.
[1] Calculation of moment of inertia
For an object that rotates around the shaft, virtually divide the object into small segments and square the
distance from the shaft to each segment. Then, sum the squares of the distances and the masses of the
segments to calculate the moment of inertia. The moment of inertia J can be calculated as follows:
J = Σ(Wi • ri
2
) (kg • m
2
) (10.11)
The following describes equations to calculate moment of inertia having different shaped loads or load
systems.
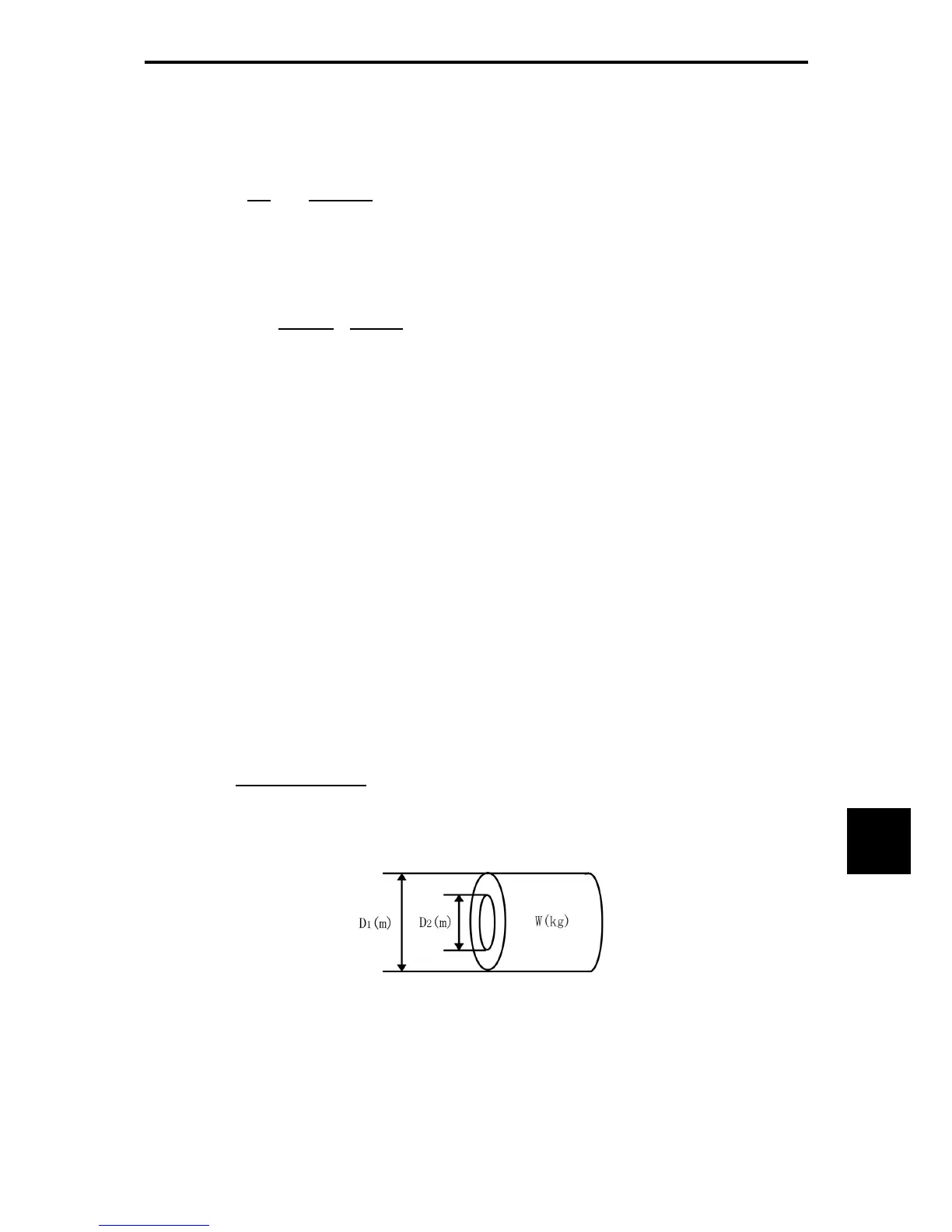
(1) Hollow cylinder and solid cylinder
The common shape of a rotating body is hollow cylinder. The moment of inertia J (kg • m
2
) around the
hollow cylinder center axis can be calculated as follows, where the outer and inner diameters are D
1
and
D
2
[m] respectively and total mass is W [kg] in Figure 10.1-10.
For a similar shape, a solid cylinder, calculate the moment of inertia as D
2
is 0.
Figure 10.1-10 Hollow cylinder
(2) For a general rotating body
Table 10.1-1 lists the calculation equations of moment of inertia J of various rotating bodies (kg • m2)
including the above cylindrical rotating body.
J 2π • N
E =
2
• (
60
)
2
(J) (10.9)
2Ï€ dN
Ï„ = J
•
60
(
dt
) (N • m) (10.10)
W • (D
1
2
+ D
2
2
)
J=
8
(kg • m
2
) (10.12)
To Next Page
Loading...
Need help?
General
